题目内容
已知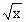
＝|cosπt－sinπt|，
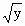＝|cos2πt－sin2πt|，其中－1≤t≤1．
(1)作出函数x＝f(t)的图象．
(2)写出y＝g(x)的解析式并作出y＝g(x)的图象．
答案：
解析：
解析：
|
解：(1)x＝cos2πt－2sinπtcosπt＋sin2πt＝1－sin2πt 所以x＝f(t)＝1－sin2πt(－1≤t≤1)的图象如图(1)所示： (2)由 所以y＝cos22πt＝1－sin22πt，由(1)知sin2πt＝1－x(0≤x≤2)．所以y＝1－(1－x)2＝－x2＋2x(0≤x≤2)． 其图象如图(2)所示：
|
＝|cos2πt|
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
＝
，求
的值．
(0，－1)和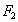
(0，1)，直线y＝4是该椭圆的一条准线．
＝1，求tan∠