题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解: 由 ∴f(x)的单调增区是(
∴方程f(x)=0有唯一实根………………(8分) |
(2) |
解:∵y=f(|x|)为偶函数 ∴只需讨论x≥0时方程f(|x|)=0的实根的个数 (1)当a=1时,f(x)=0有唯一实根x=1; (2)当0<a<1,易求得f(x)的单调增区间为(0,
综上可知:当0<a< 当a= 当 |

练习册系列答案
相关题目


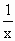 +2的图像关于点A(0,1)对称.
+2的图像关于点A(0,1)对称.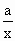 ,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间(0,2]上为减函数,求实数a的取值范围.