题目内容
设函数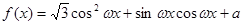 (其中
(其中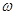 >0,
>0,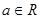 ),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
),且f(x)的图象在y轴右侧的第一个最高点的横坐标为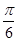 .
.
(1)求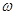 的值;
的值;
(2)如果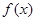 在区间
在区间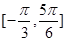 的最小值为
的最小值为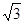 ,求
,求 的值.
的值.
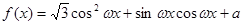 (其中
(其中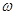 >0,
>0,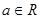 ),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
),且f(x)的图象在y轴右侧的第一个最高点的横坐标为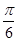 .
.(1)求
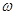 的值;
的值;(2)如果
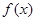 在区间
在区间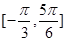 的最小值为
的最小值为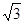 ,求
,求 的值.
的值.(1) =
= ;(2)a=
;(2)a= .
.
 =
= ;(2)a=
;(2)a= .
.试题分析:(1)对函数
 进行化简,得到f(x)==sin(2
进行化简,得到f(x)==sin(2 x+
x+ )+
)+ +a,得到2
+a,得到2 ·
· +
+ =
= ,即可求出
,即可求出 的值;(2)由(1)知f(x)=sin(2
的值;(2)由(1)知f(x)=sin(2 x+
x+ )+
)+ +a,当x∈
+a,当x∈ 时,x+
时,x+ ∈
∈ ,故-
,故- ≤sin(x+
≤sin(x+ )≤1,从而f(x)在
)≤1,从而f(x)在 上取得最小值-
上取得最小值- +
+ +a,因此,由题设知-
+a,因此,由题设知- +
+ +a=
+a= ,即可求出a的值.
,即可求出a的值.解:(1) f(x)=
 cos2
cos2 x+
x+ sin2
sin2 x+
x+ +a .2
+a .2=sin(2
 x+
x+ )+
)+ +a ..4
+a ..4依题意得2
 ·
· +
+ =
= 解得
解得 =
= .6
.6(2) 由(1)知f(x)=sin(2
 x+
x+ )+
)+ +a
+a又当x∈
 时,x+
时,x+ ∈
∈ 8
8故-
 ≤sin(x+
≤sin(x+ )≤1 ..10
)≤1 ..10从而f(x)在
 上取得最小值-
上取得最小值- +
+ +a
+a因此,由题设知-
 +
+ +a=
+a= 故a=
故a= .12
.12
练习册系列答案
相关题目

 的图形向右平移
的图形向右平移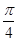 个单位后得到
个单位后得到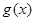 的图像,已知
的图像,已知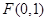 ,与x轴相交于点P、Q,点M为最高点,且
,与x轴相交于点P、Q,点M为最高点,且 的面积为
的面积为 .
.
 中,
中, 分别是角A,B,C的对边,
分别是角A,B,C的对边,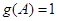 ,且
,且 ,求
,求 ,
, 并求
并求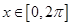 时,求f(x)的最小值以及取得最小值时x的集合.
时,求f(x)的最小值以及取得最小值时x的集合. ),y=f(x)的部分图象如图所示,则f(
),y=f(x)的部分图象如图所示,则f( )=______.
)=______.
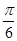 ),则下列结论正确的是( )
),则下列结论正确的是( )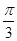 对称
对称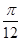 ]上为增函数
]上为增函数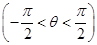 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P ,则φ的值可以是( )
,则φ的值可以是( )



 的图像向右平移
的图像向右平移 个单位,再将图像上每一点横坐标缩短到原来的
个单位,再将图像上每一点横坐标缩短到原来的 倍,所得图像关于直线
倍,所得图像关于直线 对称,则
对称,则 的最小正值为 .
的最小正值为 . ( )
( ) 、
、 上递增,在
上递增,在 、
、 上递减
上递减 上递增,在
上递增,在 上递减
上递减 、
、 上递增,在
上递增,在 、
、