题目内容
若f（x）=x2+ax+2有两个不同的零点，则实数a的取值范围是________．
分析：函数f（x）有两个零点等价于方程f（x）=0有两个不等实根，由此可解．
解答：f（x）=x2+ax+2有两个不同的零点，即方程x2+ax+2=0有两个不等实根，
所以△=a2-4×2＞0，解得a
或
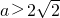．所以实数a的取值范围是（-∞，-2
）∪（2，+∞）．故答案为：（-∞，-2
）∪（2，+∞）．点评：本题考查函数零点的概念，函数f（x）的零点即为方程f（x）=0的根，注意零点不是点，是实数．
练习册系列答案
相关题目
若f（x）=x2+a，则下列判断正确的是（ ）
A、f（
| ||||
B、f（
| ||||
C、f（
| ||||
D、f（
|
）=3，则a的值为