题目内容
电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独闯第一关、第二关、第三关成功的概率分别为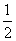 、
、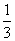 、
、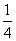 ,记该参加者闯三关所得总分为ξ.
,记该参加者闯三关所得总分为ξ.
(1) 求该参加者有资格闯第三关的概率;
(2) 求ξ的分布列和数学期望.
解:(1) 设该参加者单独闯第一关、第二关、第三关成功的概率分别为
p1=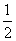 ,p2=
,p2=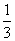 ,p3=
,p3=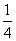 ,该参加者有资格闯第三关为事件A.
,该参加者有资格闯第三关为事件A.
则P(A)=p1(1-p2)+(1-p1)p2+p1p2=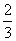 .
.
(2) 由题意可知,ξ的可能取值为0,3,6,7,10,
P(ξ=0)=(1-p1)(1-p2)=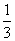 ,
,
P(ξ=3)=p1(1-p2)(1-p3)+(1-p1)p2(1-p3)=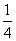 +
+ =
=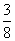 ,
,
P(ξ=6)=p1p2(1-p3)= ,
,
P(ξ=7)=p1(1-p2)p3+(1-p1)p2p3=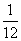 +
+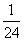 =
= ,P(ξ=10)=p1p2p3=
,P(ξ=10)=p1p2p3=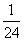 ,
,
∴ ξ的分布列为
| ξ | 0 | 3 | 6 | 7 | 10 |
| p |
|
|
|
|
|

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 .
.
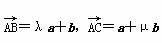 (λ、μ∈R),当A、B、C三点共线时λ、μ满足的条件为________.
(λ、μ∈R),当A、B、C三点共线时λ、μ满足的条件为________. 中随机抽取一个数记为a,从{-1,1,-2,2}中随机抽取一个数记为b,则函数y=ax+b的图象经过第三象限的概率是________.
中随机抽取一个数记为a,从{-1,1,-2,2}中随机抽取一个数记为b,则函数y=ax+b的图象经过第三象限的概率是________.