题目内容
已知a是f(x)=2x-log x的零点,若0<x0<a,则f(x0)的值与0的大小关系是________.
x的零点,若0<x0<a,则f(x0)的值与0的大小关系是________.
f(x0)<0
分析:由题意得,函数的零点就是方程的根,也即是函数图象与x轴交点的横坐标.又知函数的单调性,即可求出
f(x0)的正负.
解答:由于a是函数f(x)=2x-log x的零点,则f(a)=0,
x的零点,则f(a)=0,
又因为函数f(x)=2x -log x=2x +log2x在(0,+∞)上是增函数,
x=2x +log2x在(0,+∞)上是增函数,
所以当0<x0<a时,f(x0)<f(a),即f(x0)<0.
故答案为 f(x0)<0.
点评:本题主要考查函数的零点及函数的单调性,函数的零点的研究就可转化为相应方程根的问题,函数与方程的思想得到了很好的体现,属于基础题.
分析:由题意得,函数的零点就是方程的根,也即是函数图象与x轴交点的横坐标.又知函数的单调性,即可求出
f(x0)的正负.
解答:由于a是函数f(x)=2x-log
 x的零点,则f(a)=0,
x的零点,则f(a)=0,又因为函数f(x)=2x -log
 x=2x +log2x在(0,+∞)上是增函数,
x=2x +log2x在(0,+∞)上是增函数,所以当0<x0<a时,f(x0)<f(a),即f(x0)<0.
故答案为 f(x0)<0.
点评:本题主要考查函数的零点及函数的单调性,函数的零点的研究就可转化为相应方程根的问题,函数与方程的思想得到了很好的体现,属于基础题.

练习册系列答案
相关题目
已知t是f(x)=2-x-log
x的零点,x0>t,则f(x0)的值满足( )
| 1 |
| 2 |
| A、f(x0)=0 |
| B、f(x0)>0 |
| C、f(x0)<0 |
| D、f(x0)的符号不确定 |
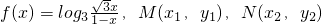 是f(x)图象上的两点,横坐标为
是f(x)图象上的两点,横坐标为 的点P满足
的点P满足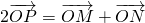 (O为坐标原点).
(O为坐标原点).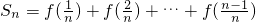 ,其中n∈N*,n≥2令
,其中n∈N*,n≥2令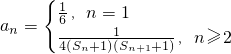 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.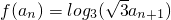 ,且
,且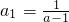 ?若存在,求出a满足的条件;若不存在,请说明理由.
?若存在,求出a满足的条件;若不存在,请说明理由.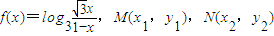 是f(x)图象上的两点,横坐标为
是f(x)图象上的两点,横坐标为 的点P满足
的点P满足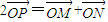 (O为坐标原点).
(O为坐标原点).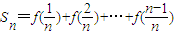 ,其中n∈N*,n≥2令
,其中n∈N*,n≥2令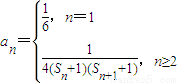 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.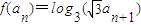 ,且
,且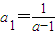 ?若存在,求出a满足的条件;若不存在,请说明理由.
?若存在,求出a满足的条件;若不存在,请说明理由.