题目内容
已知函数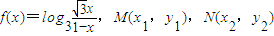 是f(x)图象上的两点,横坐标为
是f(x)图象上的两点,横坐标为 的点P满足
的点P满足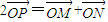 (O为坐标原点).
(O为坐标原点).(1)求证:y1+y2为定值;
(2)若
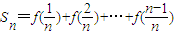 ,其中n∈N*,n≥2令
,其中n∈N*,n≥2令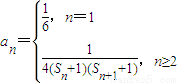 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.(3)对于给定的实数a(a>1)是否存在这样的数列{an},使得
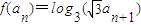 ,且
,且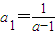 ?若存在,求出a满足的条件;若不存在,请说明理由.
?若存在,求出a满足的条件;若不存在,请说明理由.
【答案】分析:(1)设P点坐标为 ,由已知的向量关系得出x1+x2=1,利用对数运算即可求得y1+y2为定值;
,由已知的向量关系得出x1+x2=1,利用对数运算即可求得y1+y2为定值;
(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1.得出 ,下面对n进行分类讨论:当n≥2时,当n=1时,得到:
,下面对n进行分类讨论:当n≥2时,当n=1时,得到: 再利用数列求和得出Tn,结合Tn<m(Sn+1+1)对一切n∈N*都成立结合基本不等式即可求得m的取值范围;
再利用数列求和得出Tn,结合Tn<m(Sn+1+1)对一切n∈N*都成立结合基本不等式即可求得m的取值范围;
(3)对于存在性问题,可先假设存在,即假设存在数列{an}满足条件,再利用等差数列的性质,求出an的长,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)设P点坐标为 ,由已知可得,
,由已知可得, 则
则 ,
,
∴x1+x2=1 =
=
(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1. ,①
,① ,②,
,②,
∴2Sn=n-1,故
当n≥2时, .
.
又当n=1时, ,所以
,所以
故
∵Tn<m(Sn+1+1)对一切n∈N*都成立.
∴ ,而
,而 (当且仅当n=2时等号成立)
(当且仅当n=2时等号成立)
∴ ,即m的取值范围是
,即m的取值范围是
(3)假设存在数列{an}满足条件,则 ,
,
即 ,∴
,∴ 是以
是以 为首项,-1为公差的等差数列,
为首项,-1为公差的等差数列,
于是 ,∴
,∴ ,注意到
,注意到
∴当a>3时,存在这样的有穷数列{an};当1<a≤3时,不存在这样的数列.
点评:本小题主要考查等差数列的应用、数列与不等式的综合、数列的求和等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
 ,由已知的向量关系得出x1+x2=1,利用对数运算即可求得y1+y2为定值;
,由已知的向量关系得出x1+x2=1,利用对数运算即可求得y1+y2为定值;(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1.得出
 ,下面对n进行分类讨论:当n≥2时,当n=1时,得到:
,下面对n进行分类讨论:当n≥2时,当n=1时,得到: 再利用数列求和得出Tn,结合Tn<m(Sn+1+1)对一切n∈N*都成立结合基本不等式即可求得m的取值范围;
再利用数列求和得出Tn,结合Tn<m(Sn+1+1)对一切n∈N*都成立结合基本不等式即可求得m的取值范围;(3)对于存在性问题,可先假设存在,即假设存在数列{an}满足条件,再利用等差数列的性质,求出an的长,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)设P点坐标为
 ,由已知可得,
,由已知可得, 则
则 ,
,∴x1+x2=1
 =
=
(2)由(1)知当x1+x2=1时,y1+y2=f(x1)+f(x2)=1.
 ,①
,① ,②,
,②,∴2Sn=n-1,故

当n≥2时,
 .
.又当n=1时,
 ,所以
,所以
故

∵Tn<m(Sn+1+1)对一切n∈N*都成立.
∴
 ,而
,而 (当且仅当n=2时等号成立)
(当且仅当n=2时等号成立)∴
 ,即m的取值范围是
,即m的取值范围是
(3)假设存在数列{an}满足条件,则
 ,
,即
 ,∴
,∴ 是以
是以 为首项,-1为公差的等差数列,
为首项,-1为公差的等差数列,于是
 ,∴
,∴ ,注意到
,注意到
∴当a>3时,存在这样的有穷数列{an};当1<a≤3时,不存在这样的数列.
点评:本小题主要考查等差数列的应用、数列与不等式的综合、数列的求和等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是( )
| A、奇函数 | B、偶函数 | C、增函数 | D、减函数 |
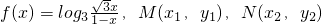 是f(x)图象上的两点,横坐标为
是f(x)图象上的两点,横坐标为 的点P满足
的点P满足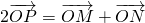 (O为坐标原点).
(O为坐标原点).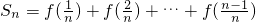 ,其中n∈N*,n≥2令
,其中n∈N*,n≥2令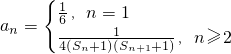 ,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.
,其中n∈N*,Tn为数列{an}的前n项和,若Tn<m(Sn+1+1)对一切n∈N*都成立,试求m的取值范围.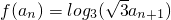 ,且
,且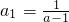 ?若存在,求出a满足的条件;若不存在,请说明理由.
?若存在,求出a满足的条件;若不存在,请说明理由.