题目内容
设无穷等比数列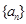 的公比为q,且
的公比为q,且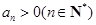 ,
,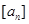 表示不超过实数
表示不超过实数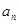 的最大整数(如
的最大整数(如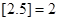 ),记
),记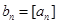 ,数列
,数列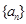 的前
的前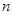 项和为
项和为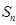 ,数列
,数列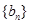 的前
的前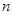 项和为
项和为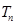 .
.
(Ⅰ)若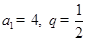 ,求
,求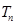 ;
;
(Ⅱ)若对于任意不超过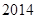 的正整数n,都有
的正整数n,都有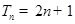 ,证明:
,证明: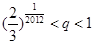 .
.
(Ⅲ)证明: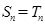 (
(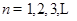 )的充分必要条件为
)的充分必要条件为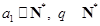 .
.
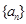 的公比为q,且
的公比为q,且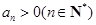 ,
,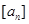 表示不超过实数
表示不超过实数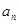 的最大整数(如
的最大整数(如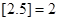 ),记
),记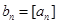 ,数列
,数列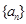 的前
的前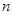 项和为
项和为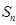 ,数列
,数列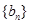 的前
的前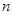 项和为
项和为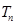 .
.(Ⅰ)若
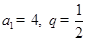 ,求
,求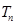 ;
;(Ⅱ)若对于任意不超过
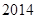 的正整数n,都有
的正整数n,都有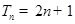 ,证明:
,证明: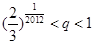 .
.(Ⅲ)证明:
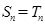 (
(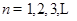 )的充分必要条件为
)的充分必要条件为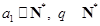 .
.(Ⅰ)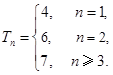 ;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.
;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.
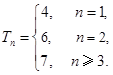 ;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.
;(Ⅱ)答案详见解析;(Ⅲ)答案详见解析.试题分析:(Ⅰ)由已知得,
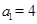 ,
,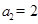 ,
,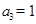 ,且当
,且当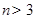 时,
时,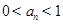 .且
.且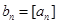 ,故
,故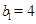 ,
,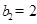 ,
,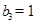 ,且当
,且当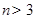 时,
时,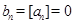 ,进而求
,进而求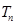 ;(Ⅱ)已知数列
;(Ⅱ)已知数列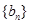 的前
的前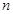 项和
项和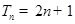 (
(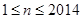 ),可求得
),可求得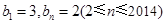 ,由取整函数得
,由取整函数得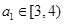 ,
,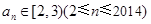 ,故
,故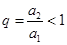 ,要证明
,要证明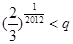 ,只需证明
,只需证明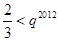 ,故可联想到
,故可联想到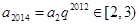 ,则
,则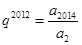
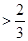 ;(Ⅲ)先证明充分性,当
;(Ⅲ)先证明充分性,当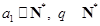 时,
时,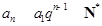 ,由取整函数的性质得
,由取整函数的性质得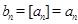 ,故
,故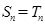 ;必要性的证明,当
;必要性的证明,当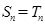 时,
时,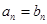 ,则有
,则有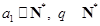 .
.试题解析:(Ⅰ)解:由等比数列
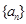 的
的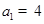 ,
,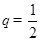 ,得
,得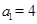 ,
,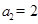 ,
,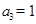 ,且当
,且当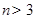 时,
时,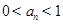 .
. 所以
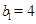 ,
,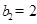 ,
,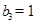 ,且当
,且当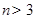 时,
时,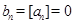 .
.即
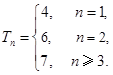
(Ⅱ)证明:因为
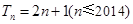 ,所以
,所以 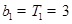 ,
,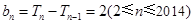 .
.因为
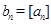 ,
,所以
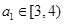 ,
,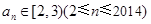 .
. 由
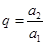 ,得
,得 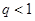 .
.因为
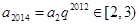 ,
,所以
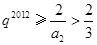 ,
,所以
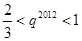 ,即
,即 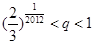 .
.(Ⅲ)证明:(充分性)因为
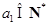 ,
,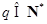 ,
,所以
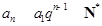 ,
,所以
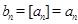 对一切正整数n都成立.
对一切正整数n都成立.因为
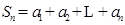 ,
,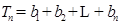 ,
,所以
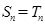 .
.(必要性)因为对于任意的
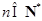 ,
,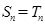 ,
,当
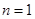 时,由
时,由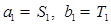 ,得
,得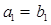 ;
;当
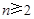 时,由
时,由 ,
,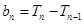 ,得
,得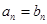 .
.所以对一切正整数n都有
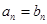 .
.由
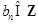 ,
,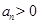 ,得对一切正整数n都有
,得对一切正整数n都有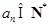 ,
,所以公比
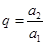 为正有理数.
为正有理数.假设
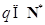 ,令
,令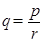 ,其中
,其中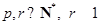 ,且
,且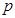 与
与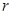 的最大公约数为1.
的最大公约数为1. 因为
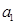 是一个有限整数,
是一个有限整数,所以必然存在一个整数
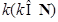 ,使得
,使得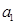 能被
能被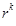 整除,而不能被
整除,而不能被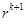 整除.
整除.又因为
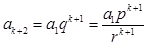 ,且
,且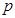 与
与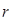 的最大公约数为1.
的最大公约数为1. 所以
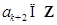 ,这与
,这与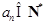 (
(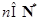 )矛盾.
)矛盾.所以
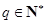 .
.因此
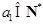 ,
,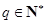 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
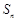 是等比数列
是等比数列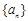 的前
的前 项和,
项和,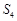 、
、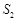 、
、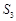 成等差数列,且
成等差数列,且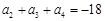 .
.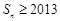 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有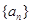 的前
的前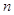 项和为
项和为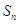 ,且
,且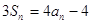 .
.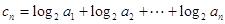 ,
,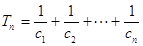 ,求使
,求使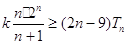 恒成立的实数
恒成立的实数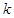 的取值范围.
的取值范围.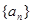 的前n项和为
的前n项和为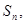
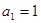 ,
,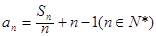
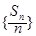 为等差数列;
为等差数列;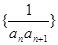 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.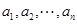 为
为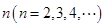 阶“期待数列”:
阶“期待数列”: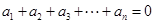 ;②
;②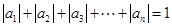 .
.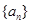 的通项公式是
的通项公式是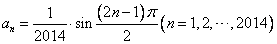 ,
,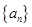 为
为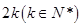 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及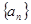 前
前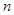 项和
项和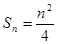 ,数列
,数列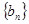 满足
满足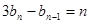 (
(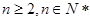 ),
),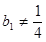 时,数列
时,数列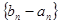 为等比数列;
为等比数列;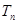 ,若数列
,若数列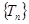 中只有
中只有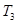 最小,求
最小,求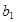 的取值范围.
的取值范围. 中,已知对任意正整数
中,已知对任意正整数 ,
, ,则
,则 等于( )
等于( )



 和
和 的等比中项是 .
的等比中项是 .