题目内容
在△ABC中，∠C是钝角，设x=sinC，y=sinA+sinB，z=cosA+cosB，则x，y，z的大小关系是分析：不妨令A=120°，B=C=30°，分别求出x，y，z 的值，从而求得x，y，z的大小关系．
解答：解：不妨令C=120°，B=A=30°，则x=sinC=
，y=sinA+sinB=
+
=1，
z=cosA+cosB=
+
=
，故有x＜y＜z，
故答案为：x＜y＜z．
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
z=cosA+cosB=
| ||
| 2 |
| ||
| 2 |
| 3 |
故答案为：x＜y＜z．
点评：本题考查在限定条件下比较式子的大小的方法，用特殊值代入法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，C是直角，则sin2A+2sinB（ ）
| A、有最大值无最小值 | B、有最小值无最大值 | C、有最大值也有最小值 | D、无最大值也无最小值 |
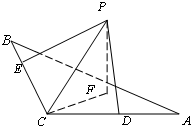如图，在△ABC中，∠C是直角，平面ABC外有一点P，PC=24，点P到直线AC、BC的距离PD和PE都等于6
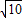，求：