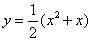题目内容
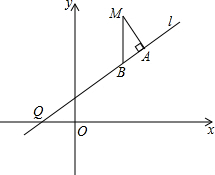 已知曲线C是到点P(-
已知曲线C是到点P(-| 1 |
| 2 |
| 3 |
| 8 |
| 5 |
| 8 |
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线l的方程,使得
| |QB|2 |
| |QA| |
分析:(I)设N(x,y)为C上的点,进而可表示出|NP|,根据N到直线y=-
的距离和|NP|进而可得曲线C的方程.
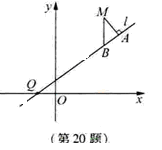
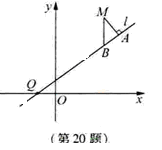
(II)先设M(x,
),直线l:y=kx+k,进而可得B点坐标,再分别表示出|QB|,|QM|,|MA|,最后根据|QA|2=|QM|2-|AM|2求得k.
| 5 |
| 8 |
(II)先设M(x,
| x2+x |
| 2 |
解答: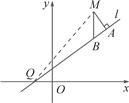 解:(I)设N(x,y)为C上的点,则|NP|=
解:(I)设N(x,y)为C上的点,则|NP|=
,
N到直线y=-
的距离为|y+
|.
由题设得
=|y+
|,
化简,得曲线C的方程为y=
(x2+x).
(II)设M(x,
),直线l:y=kx+k,则B(x,kx+k),从而|QB|=
|x+1|.
在Rt△QMA中,因为|QM | 2= (x+1)2+(
) 2=(x+1)2(1+
),|MA| 2=
.
所以|QA|2=|QM|2-|AM|2=
(kx+2)2,
∴|QA|=
,
=
•|
|.
当k=2时,
=5
,
从而所求直线l方程为2x-y+2=0.
 解:(I)设N(x,y)为C上的点,则|NP|=
解:(I)设N(x,y)为C上的点,则|NP|=(x+
|
N到直线y=-
| 5 |
| 8 |
| 5 |
| 8 |
由题设得
(x+
|
| 5 |
| 8 |
化简,得曲线C的方程为y=
| 1 |
| 2 |
(II)设M(x,
| x2+x |
| 2 |
| 1+k2 |
在Rt△QMA中,因为|QM | 2= (x+1)2+(
| x2+x |
| 2 |
| x2 |
| 4 |
(x+1)2(k-
| ||
| 1+k2 |
所以|QA|2=|QM|2-|AM|2=
| (x+1)2 |
| 4(1+k2) |
∴|QA|=
| |x+1|•|kx+2| | ||
2
|
| |QB|2 |
| |QA| |
2(1+k2)
| ||
| |k| |
| x+1 | ||
x+
|
当k=2时,
| |QB|2 |
| |QA| |
| 5 |
从而所求直线l方程为2x-y+2=0.
点评:本题主要考查求曲线轨迹方程,两条直线的位置关系等基础知识,考查解析几何的基本思想方法和综合解题能力.

练习册系列答案
相关题目