题目内容
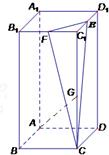 在正四棱柱ABCD-A1B1C1D1中,E,F分别是C1D1,C1B1的中点,G为CC1上任一点,EC与底面ABCD所成角的正切值是4.
在正四棱柱ABCD-A1B1C1D1中,E,F分别是C1D1,C1B1的中点,G为CC1上任一点,EC与底面ABCD所成角的正切值是4.(Ⅰ)求证AG⊥EF;
(Ⅱ)确定点G的位置,使AG⊥面CEF,并说明理由;
(Ⅲ)求二面角F-CE-C1的余弦值.
分析:本题考查的知识点是平面与平面间的位置关系.由ABCD-A1B1C1D1为正四棱柱ABCD-A1B1C1D1,故我们可以设底面边长为2a,又由EC与底面ABCD所成角的正切值是4,我们易求出侧棱长为4a,以A为原点,AB、AD、AA1所在的直线分别为x轴,y轴,z轴,空间直角坐标系.给出正四棱柱中各顶点的坐标,使用向量法进行证明和求解:
(1)要证明AG⊥EF,我们仅需要证明
⊥
,即
•
=0即可.
(2)由(1)的结论,要使AG⊥面CEF,只需AG⊥CE,即证明
•
=0即可;
(3)求二面角F-CE-C1的余弦值,由
是平面CEF的一个法向量,
是平面CEC1的一个法向量,我们只要求出向量
与
夹角余弦值的绝对值即可,解三角形ADG不难得到结论.
(1)要证明AG⊥EF,我们仅需要证明
| AG |
| EF |
| AG |
| EF |
(2)由(1)的结论,要使AG⊥面CEF,只需AG⊥CE,即证明
| AG |
| CE |
(3)求二面角F-CE-C1的余弦值,由
| AG |
| AD |
| AG |
| AD |
解答: 解:∵ABCD-A1B1C1D1是正四棱柱
解:∵ABCD-A1B1C1D1是正四棱柱
∴ABCD是正方形,设其边长为2a,?ECD是EC与底面所成的角.而∠ECD=∠CEC1,
∴CC1=4EC1=4a.
以A为原点,AB、AD、AA1所在的直线分别为x轴,y轴,z轴,建立如图所示的直角坐标系.
则A(0,0,0),B(2a,0,0),C(2a,2a,0),D(0,2a,0),
A1(0,0,4a),B1(2a,0,4a),C1(2a,2a,4a),D1(0,2a,4a),
E(a,2a,4a),F(2a,a,4a),设G(2a,2a,b)(0<b<4a)
(Ⅰ)
=(2a,2a,b),
=(a,-a,0),
•
=2a2-2a2+0=0,
∴AG⊥EF
(Ⅱ)由(Ⅰ)知,使AG⊥面CEF,只需AG⊥CE,
只需
•
=(2a,2a,b)×(-a,0,4a)=-2a2+4ab=0,
∴b=
a,即CG=
CC1时,AG⊥面CEF.
(Ⅲ)由(Ⅱ)知,当G(2a,2a,
a)时,
是平面CEF的一个法向量,
由题意可得,
是平面CEC1的一个法向量,
设二面角F-CE-C1的大小为q,
则cosq=
=
=
,
二面角F-CE-C1的余弦值为
.
 解:∵ABCD-A1B1C1D1是正四棱柱
解:∵ABCD-A1B1C1D1是正四棱柱∴ABCD是正方形,设其边长为2a,?ECD是EC与底面所成的角.而∠ECD=∠CEC1,
∴CC1=4EC1=4a.
以A为原点,AB、AD、AA1所在的直线分别为x轴,y轴,z轴,建立如图所示的直角坐标系.
则A(0,0,0),B(2a,0,0),C(2a,2a,0),D(0,2a,0),
A1(0,0,4a),B1(2a,0,4a),C1(2a,2a,4a),D1(0,2a,4a),
E(a,2a,4a),F(2a,a,4a),设G(2a,2a,b)(0<b<4a)
(Ⅰ)
| AG |
| EF |
| AG |
| EF |
∴AG⊥EF
(Ⅱ)由(Ⅰ)知,使AG⊥面CEF,只需AG⊥CE,
只需
| AG |
| CE |
∴b=
| 1 |
| 2 |
| 1 |
| 8 |
(Ⅲ)由(Ⅱ)知,当G(2a,2a,
| 1 |
| 2 |
| AG |
由题意可得,
| AD |
设二面角F-CE-C1的大小为q,
则cosq=
| ||||
|
|
(2a,2a,
| ||||||
|
4
| ||
| 33 |
二面角F-CE-C1的余弦值为
4
| ||
| 33 |
点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值,空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值.

练习册系列答案
相关题目
 如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,棱长AA1=2,AB=1,E是AA1的中点. 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,AA1=2,M、N分别为B1B和A1D的中点.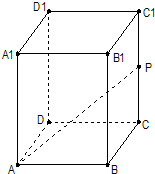 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)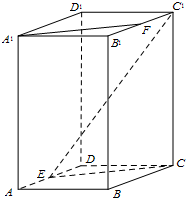 (2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.
(2012•昌平区二模)在正四棱柱ABCD-A1B1C1D1中,E为AD中点,F为B1C1中点.