题目内容
16.若$\overrightarrow{a}$=(λ,2),$\overrightarrow{b}$=(-3,5),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角,则λ的取值范围是( )| A. | ($\frac{10}{3}$,+∞) | B. | [$\frac{10}{3}$,+∞) | C. | (-∞,$\frac{10}{3}$) | D. | (-∞,$\frac{10}{3}$] |
分析 根据题意,由向量数量积的性质分析可得有$\overrightarrow{a}$•$\overrightarrow{b}$=(-3)λ+2×5<0,且5λ≠2×(-3),解可得λ的取值范围,即可得答案.
解答 解:根据题意,$\overrightarrow{a}$=(λ,2),$\overrightarrow{b}$=(-3,5),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是钝角,
则有$\overrightarrow{a}$•$\overrightarrow{b}$=(-3)λ+2×5<0,且5λ≠2×(-3),
解可得λ>$\frac{10}{3}$,
即λ的取值范围是($\frac{10}{3}$,+∞);
故选:A.
点评 本题考查向量数量积的坐标运算,涉及向量夹角的判定,注意排除两个向量反向的情况.

练习册系列答案
相关题目
8.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x单位:小时)与当天投篮命中率y之间的关系:
(1)用线性回归分析的方法求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.(2)预测小李该月6号打6小时篮球的投篮命中率.
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
| 时间x | 1 | 2 | 3 | 4 | 5 |
| 命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
$\left\{\begin{array}{l}{\stackrel{∧}{b}=\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}}\\{\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}}\end{array}\right.$.
5.一个各面均涂有油漆的正方体(魔方)被锯成27个同样大小的小正方体,将这些小正方体均匀的搅混在一起,现任意的取出一个小正方体,则事件“小正方体的三个面上有油漆”的概率是( )
| A. | $\frac{12}{27}$ | B. | $\frac{6}{27}$ | C. | $\frac{1}{27}$ | D. | $\frac{8}{27}$ |
6.2016年春晚过后,为了研究演员上春晚次数与受关注度的关系,某站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(Ⅰ)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并就此分析:该演员上春晚11次时的粉丝数量;
(Ⅱ)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选2组,求这两组数据之和不超过15的概率.
参考公式:$\begin{array}{l}用最小二乘法求线性回归方程系数公式:\\ \widehatb=\frac{{\sum_{i-1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i-1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i-1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i-1}^n{{{({{x_i}-\overline x})}^2}}}},\widehata=\overline y-b\overline x\end{array}$.
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(Ⅱ)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(精确到整数):
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选2组,求这两组数据之和不超过15的概率.
参考公式:$\begin{array}{l}用最小二乘法求线性回归方程系数公式:\\ \widehatb=\frac{{\sum_{i-1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i-1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i-1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i-1}^n{{{({{x_i}-\overline x})}^2}}}},\widehata=\overline y-b\overline x\end{array}$.
 如图,PA=PC,∠APC=∠ACB=90°,∠BAC=60°,平面PAC⊥平面ABC.
如图,PA=PC,∠APC=∠ACB=90°,∠BAC=60°,平面PAC⊥平面ABC.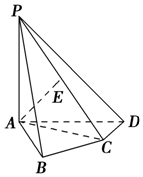 如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.