题目内容
已知向量 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线 对称,且
对称,且 .
.
(Ⅰ)求f(x)的最小正周期及单调递增区间;
(Ⅱ)函数的图象经过怎样的平移变换能使所得图象对应的函数为偶函数?
解:(Ⅰ)∵ =
=
= ,
,
∵ ,∴
,∴ ,
,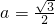 .
.
又函数f(x)的图象关于直线 对称,故有
对称,故有 ,即
,即  ,b=1.
,b=1.
∴ ,故周期T=π.
,故周期T=π.
当f(x)单调递增时,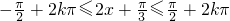 (k∈Z),
(k∈Z),
解得 ,
,
∴f(x)的单调递增区间是 .
.
(Ⅱ) ,
,
∴f(x)的图象向左平移 个单位,可得偶函数y=cos2x 的图象.
个单位,可得偶函数y=cos2x 的图象.
分析:(Ⅰ)利用两个向量的数量积公式化简函数f(x)的解析式,再由 以及
以及 ,进一步确定函数的解析式为
,进一步确定函数的解析式为 ,由此求出最小正周期以及单调增区间.
,由此求出最小正周期以及单调增区间.
(Ⅱ)把函数f(x)的解析式利用诱导公式化为 ,
,
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,正弦函数的单调性和周期性,属于中档题.
 =
=
=
 ,
,∵
 ,∴
,∴ ,
,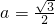 .
.又函数f(x)的图象关于直线
 对称,故有
对称,故有 ,即
,即  ,b=1.
,b=1.∴
 ,故周期T=π.
,故周期T=π.当f(x)单调递增时,
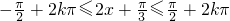 (k∈Z),
(k∈Z),解得
 ,
,∴f(x)的单调递增区间是
 .
.(Ⅱ)
 ,
,∴f(x)的图象向左平移
 个单位,可得偶函数y=cos2x 的图象.
个单位,可得偶函数y=cos2x 的图象.分析:(Ⅰ)利用两个向量的数量积公式化简函数f(x)的解析式,再由
 以及
以及 ,进一步确定函数的解析式为
,进一步确定函数的解析式为 ,由此求出最小正周期以及单调增区间.
,由此求出最小正周期以及单调增区间.(Ⅱ)把函数f(x)的解析式利用诱导公式化为
 ,
,点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,正弦函数的单调性和周期性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
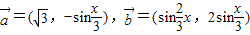 ,函数f(x)=
,函数f(x)=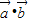 .
.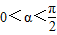 且
且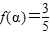 ,求
,求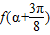 的值.
的值.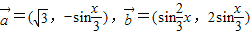 ,函数f(x)=
,函数f(x)=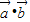 .
.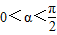 且
且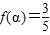 ,求
,求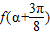 的值.
的值.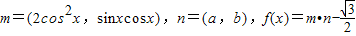 ,函数f(x)的图象关于直线
,函数f(x)的图象关于直线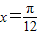 对称,且
对称,且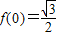
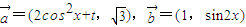 ,函数f(x)=
,函数f(x)=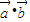 .
.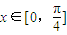 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.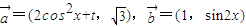 ,函数f(x)=
,函数f(x)=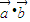 .
.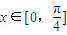 时,f(x)有最大值4,求实数t的值.
时,f(x)有最大值4,求实数t的值.