题目内容
【题目】已知函数
.
（1）若
的图像过点
，且在点
处的切线方程为
，试求函数的单调区间；
（2）当
时，若函数
恒成立，求整数
的最小值.
【答案】（1）函数的单调递增区间为
，单调递减区间为
（2）1
【解析】
（1）根据
且
求得函数解析式，分别令
求得
的范围，可得函数
增区间，
求得的范围，可得函数的减区间；（2）函数
恒成立等价于
在区间
内恒成立，根据零点存在定理确定
极值点
的范围，可得
的范围，从而可得结果.
（1）函数过点
可知
，①，
，
∴
，
，②，联立①②可得
，
所以
，函数的定义域为，
可知
，
，
，
，
可知函数的单调递增区间为，单调递减区间为
（2）由可知
，
因为
，所以原命题等价于
在区间内恒成立.
设
，
可设
，在单调递增，且
，
，
所以存在唯一的
，使得
且当
时，
，单调递增，
当
，
，单调递减，
所以当
时，有极大值，也为最大值，且
又，所以
，∴
，可知
，所以
的最小值为1.
练习册系列答案
相关题目
【题目】某公交公司为了方便市民出行、科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为研究车辆发车间隔时间
（分钟）与乘客等候人数
（人）之间的关系，经过调查得到如下数据：
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这
组数据中选取
组数据求线性回归方程，再用剩下的
组数据进行检验．检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数
，再求与实际等候人数的差，若差值的绝对值不超过
，则称所求线性回归方程是“恰当回归方程”．
（1）从这
组数据中随机选取组数据后，求剩下的组数据的间隔时间之差大于的概率；
（2）若选取的是后面组数据，求关于的线性回归方程
，并判断此方程是否是“恰当回归方程”；
（3）在（2）的条件下，为了使等候的乘客不超过
人，则间隔时间最多可以设置为多少分钟？（精确到整数）
参考公式：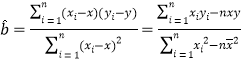
，
．