题目内容

设函数f（x）=n2x2（1-x）n（n为正整数），则f（x）在[0，1]上的最大值为
4(
n
n+2
)n+2
4(
n
n+2
)n+2
．
分析：对函数求导，令导数f′（x）=0，解得x的值，分析导函数的符号，确定函数在点x=
2
n+2
取极大值，即函数的最大值，代入函数解析式即可求得结果．
解答：解：f′（x）=2n2x（1-x）n-n×n2x2（1-x）n-1
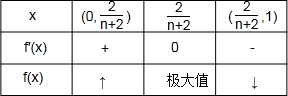
=n2x（1-x）n-1（2-2x-nx）=-n2x（1-x）n-1[（n+2）x-2]=0
得x=0，或x=1，或x=
2
n+2

f（x）在[0，1]上是x的变化情况如下：
∴f（x）在[0，1]上的最大值为4(
n
n+2
)n+2
故答案为：4(
n
n+2
)n+2
点评：此题考查利用函数的导数研究函数的最值问题，注意导数的运算法则的应用是正确解题的关键，考查运算能力，属中档题．
练习册系列答案
相关题目
已知函数f（x）=ex-kx，
（1）若k=e，试确定函数f（x）的单调区间；
（2）若k＞0，且对于任意x∈R，f（|x|）＞0恒成立，试确定实数k的取值范围；
（3）设函数F（x）=f（x）+f（-x），求证：F（1）F（2）…F（n）＞( en+1+2)
n2
（n∈N*）．
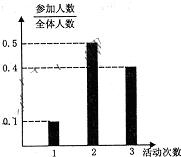精英家教网（理科）某中学号召学生在2010年春节期间至少参加一次社会公益活动（下面简称为“活动”）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．
（Ⅰ）求合唱团学生参加活动的人均次数；
（Ⅱ）从合唱团中任选两名学生，求他们参加活动次数恰好相等的概率．

（文科）先后抛掷一枚骰子两次，得到点数m，n，确定函数f（x）=x2+mx+n2，设函数f（x）有零点为事件A．
（Ⅰ）求事件A的概率P（A）；
（Ⅱ）设函数g（x）=x2+12P（A）x-4的定义域为[-5，5]，记“当x0∈[-5，5]时，则g（x0）≥0”为事件B，求事件B的概率P（B）．
设函数f（x）=xm+ax的导数f′（x）=2x+3，则数列{
1
f(n)+2
}（n∈N*）的前n项和是（　　）
设函数f（x）=a1+a2x+a3x2+…+anxn-1，f（0）=
12
，数列{an}满足f（1）=n2•an，则数列{an}的通项=
 
．
定义函数f（x）=[x[x]]，其中[x]表示不超过x的最大整数，如：[1.5]=1，[-1.3]=-2，当x∈[0，n），n∈N*时，设函数f（x）的值域为A，则集合A中的元素个数为
n2-n+2
2
n2-n+2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网