题目内容
在△ABC中，B=
，AC=
，则AB+2BC的最大值为
，AC=，则AB+2BC的最大值为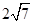 
解：设AB="c" AC="b" BC=a
由余弦定理
cosB=（a2+c2-b2）/2ac
所以a2+c2-ac=b2=3
设c+2a=m 代入上式得
7a2-5am+m2-3=0
△=84-3m2≥0 故m≤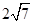
当m=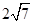时，此时a=
c=
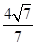符合题意
因此最大值为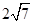
由余弦定理
cosB=（a2+c2-b2）/2ac
所以a2+c2-ac=b2=3
设c+2a=m 代入上式得
7a2-5am+m2-3=0
△=84-3m2≥0 故m≤
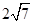
当m=
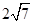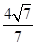时，此时a= c=符合题意因此最大值为
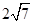
练习册系列答案
阅读快车系列答案
相关题目
中，角
所对边分别为
，若
．则
的最小值为 ．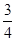
,cos(a－b)＝
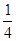,则tana·tanb＝( )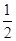
中,
,若该三角形有两解,则
的取值范围是 ．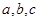
分别为角A，B，C所对的边，且
。
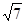，且△ABC的面积为
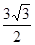，求
的值。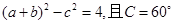
，则ab的值为（ ）
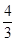B、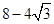
C、1 D、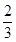
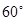，AB=2,AC=1,EF为边BC的三等分点，则
( ) 
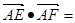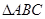中，角A、B、C的对应边分别为a、b、c，若
，
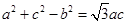中，
则
的取值范围是