题目内容
一个直角△ABC的三边分别是AC=3,BC=4,AB=5,将这个三角形绕斜边AB旋转一周,所形成的几何体的表面积是分析:由题意可知旋转体是有两个圆锥组成的几何体,求出圆锥的底面周长,即可得到几何体的表面积.
解答:解:一个直角△ABC的三边分别是AC=3,BC=4,AB=5,将这个三角形绕斜边AB旋转一周,所形成的几何体是有两个圆锥组成的几何体,圆锥的底面半径为:
;
所以几何体的表面积为:
×(
)×(3+4)=
π.
故答案为:
π
| 12 |
| 5 |
所以几何体的表面积为:
| 1 |
| 2 |
| 24π |
| 5 |
| 84 |
| 5 |
故答案为:
| 84 |
| 5 |
点评:本题是基础题,考查旋转体的表面积的求法,正确判断几何体的特征,求出底面半径是解题的关键,考查计算能力,空间想象能力.

练习册系列答案
相关题目
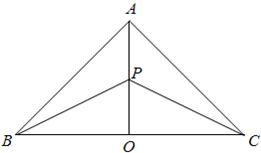 某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y. ,求y关于
,求y关于 的函数关系式;
的函数关系式;