题目内容
设AB和CD是异面直线, M和N分别是线段AB和CD的中点, 比较MN与[ ]
A.MN>![]() (BC+AD) B.MN=
(BC+AD) B.MN= ![]() (BC+AD)
(BC+AD)
C.MN<![]() (BC+AD) D.不确定
(BC+AD) D.不确定
答案:C
解析:
提示:
解析:
|
解: 连结BN并延长到E, 使NE= BN; 连结AE、DE. △ABE中, M是AB的中点, N是BE的中点, 所以AE= 2MN. 又由∠DNE= ∠CNB,ND= CN, NE= BN, 得△DNE≌△CNB, 因而DE= BC. 现在证明D点不在线段AE上. 用反证法: 假使D点在AE上, 那么由于N点在BE上, 直线ND就在平面ABE上, 即AB与CD在同一平面内, 与已知矛盾. 所以D不在AE上, 由此得AE<AD+DE, 即2MN<AD+BC.
∴MN<
|
提示:
| 连BN并延长到E, 使NE=BN, 连AE, DE. 在△ADE中, 利用AE<AD+DE. |

练习册系列答案
相关题目
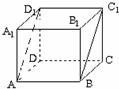 如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )| A、AD∥平面CB1D1 | B、AC1⊥BD | C、AC1⊥平面CB1D1 | D、AD1和CD是异面直线 |

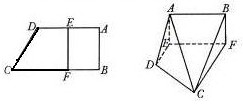 (2010•湖北模拟)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直.
(2010•湖北模拟)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直.