题目内容
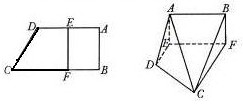 (2010•湖北模拟)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直.
(2010•湖北模拟)如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=3,BC=4,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直.(1)证明:直线AB与CD是异面直线;
(2)当直线AC与平面EFCD所成角为30°时,求二面角A-DC-E的余弦值.
分析:(1)直线AB与CD是异面直线用反证法证明:假直线AB与CD共面,由线面平行的性质定理及平行公理,我们可以得到CD与已知中ABCD为梯形矛盾,进而得到直线AB与CD是异面直线;
(2)构造∠ACE是直线AC与平面EFCD所成的角,可求EF;延长CD,EF,相交于N,过E作EH⊥DN于H,连接AH,可证得∠AHE是二面角A-DC-E的平面角,从而可求二面角A-DC-E的大小.
(2)构造∠ACE是直线AC与平面EFCD所成的角,可求EF;延长CD,EF,相交于N,过E作EH⊥DN于H,连接AH,可证得∠AHE是二面角A-DC-E的平面角,从而可求二面角A-DC-E的大小.
解答:解:(反证法)(1)假设AB,CD共面,
则AB∥CD或AB与CD相交,若AB∥CD,又AB∥EF,
则CD∥EF矛盾.若AB∩CD=P,
则P∈EF,∴AB∩EF=P,矛盾.(6分)
(2)∵AE⊥EF,平面ABEF⊥平面EFCD,
∴AE⊥平面EFCD.
∴∠ACE是直线AC与平面EFCD所成的角.∠ACE=30°,AE=2.
∴EC=2
,又FC=2,∴EF=2
.(8分)
延长CD,EF相交于N,过E作EH⊥DN于H,
连AH,则AH⊥DA.
∴∠AHE是二面角A-DE-E的平面角,又DE=1,FC=2,
则NE=EF=2
.
∴EH=
=
,tan∠AHE=
=
,cos∠AHE=
.
∴二面角A-DC-E的余弦值是
.(12分)
则AB∥CD或AB与CD相交,若AB∥CD,又AB∥EF,
则CD∥EF矛盾.若AB∩CD=P,
则P∈EF,∴AB∩EF=P,矛盾.(6分)
(2)∵AE⊥EF,平面ABEF⊥平面EFCD,
∴AE⊥平面EFCD.
∴∠ACE是直线AC与平面EFCD所成的角.∠ACE=30°,AE=2.
∴EC=2
| 3 |
| 2 |
延长CD,EF相交于N,过E作EH⊥DN于H,
连AH,则AH⊥DA.
∴∠AHE是二面角A-DE-E的平面角,又DE=1,FC=2,
则NE=EF=2
| 2 |
∴EH=
| NE•DE | ||
|
2
| ||
| 3 |
| 2 | ||||
|
3
| ||
| 2 |
| ||
| 11 |
∴二面角A-DC-E的余弦值是
| ||
| 11 |
点评:本题考查的知识点是二面角的平面角及求法,异面直线的判定,其中(1)中反证法关键是由假设结论不成立,推理后得到矛盾,(2)的关键是找出∠AHE是二面角A-DC-E的平面角,∠ACE是直线AC与平面EFCD所成的角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( ) (2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.