题目内容
 如图,在凸四边形ABCD中,AB=4,BC=3,CD=
如图,在凸四边形ABCD中,AB=4,BC=3,CD= ,且∠ADC=∠ABC=90°,则
,且∠ADC=∠ABC=90°,则 等于
等于
- A.

- B.

- C.

- D.

B
分析:由题意求得AC、AD、∠DAC的值,设∠BAC=α,则∠BAD=α+30°,可得cosα 及sinα的值,根据
 =(
=( )•
)• =
=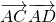 -
-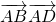 ,利用两个向量的数量积的定义求出结果.
,利用两个向量的数量积的定义求出结果.
解答:由题意可得AC=5,∠DAC=30°,AD=AC•cos30°= .
.
设∠BAC=α,则∠BAD=α+30°,cosα= =
= ,sinα=
,sinα= =
= .
.
故 =(
=( )•
)• =
=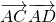 -
-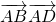
=5× cos30°-4×
cos30°-4× cos(α+30°)=
cos(α+30°)=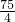 -
- (
( -
- )
)
= .
.
故选B.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.
分析:由题意求得AC、AD、∠DAC的值,设∠BAC=α,则∠BAD=α+30°,可得cosα 及sinα的值,根据
 =(
=( )•
)• =
=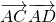 -
-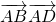 ,利用两个向量的数量积的定义求出结果.
,利用两个向量的数量积的定义求出结果.解答:由题意可得AC=5,∠DAC=30°,AD=AC•cos30°=
 .
.设∠BAC=α,则∠BAD=α+30°,cosα=
 =
= ,sinα=
,sinα= =
= .
.故
 =(
=( )•
)• =
=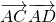 -
-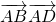
=5×
 cos30°-4×
cos30°-4× cos(α+30°)=
cos(α+30°)=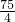 -
- (
( -
- )
)=
 .
.故选B.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
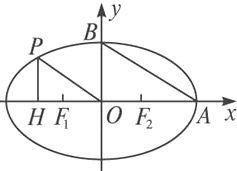 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影. 如图,在凸四边形ABCD中,AB=4,BC=3,CD=
如图,在凸四边形ABCD中,AB=4,BC=3,CD=
 如图,在凸四边形ABCD中,AB=4,BC=3,CD=
如图,在凸四边形ABCD中,AB=4,BC=3,CD= ,且∠ADC=∠ABC=90°,则
,且∠ADC=∠ABC=90°,则 等于( )
等于( )


