题目内容
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0。
(1)求证: b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值.
(1)求证: b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值.
(1)证明略(2)证明略(3) b=-4,c=3
(1)∵-1≤sinα≤1且f(sinα)≥0恒成立,∴f(1)≥0
∵1≤2+cosβ≤3,且f(2+cosβ)≤0恒成立 ∴f(1)≤0.
∴f(1)≤0.
从而知f(1)=0∴b+c+1=0
(2)由f(2+cosβ)≤0,知f(3)≤0,∴9+3b+c≤0 又因为b+c=-1,∴c≥3
又因为b+c=-1,∴c≥3
(3)∵f(sinα)=sin2α+(-1-c)sinα+c=(sinα- )2+c-(
)2+c-( )2,
)2,
当sinα=-1时,[f(sinα)]max=8,由 解得b=-4,c=3.
解得b=-4,c=3.
∵1≤2+cosβ≤3,且f(2+cosβ)≤0恒成立
 ∴f(1)≤0.
∴f(1)≤0. 从而知f(1)=0∴b+c+1=0

(2)由f(2+cosβ)≤0,知f(3)≤0,∴9+3b+c≤0
 又因为b+c=-1,∴c≥3
又因为b+c=-1,∴c≥3
(3)∵f(sinα)=sin2α+(-1-c)sinα+c=(sinα-
 )2+c-(
)2+c-( )2,
)2,当sinα=-1时,[f(sinα)]max=8,由
 解得b=-4,c=3.
解得b=-4,c=3.
练习册系列答案
相关题目
 中,
中, ,
, .
. 的大小;
的大小; ,求最小边的边长.
,求最小边的边长. .
. 的形式.
的形式. 的周期、最大值及最小值及当函数取最大值和最小值时相应的
的周期、最大值及最小值及当函数取最大值和最小值时相应的 值的集合.
值的集合.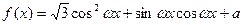 (其中
(其中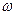 >0,
>0,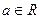 ),且
),且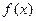 的图象在y轴右侧的第一个高点的横坐标为
的图象在y轴右侧的第一个高点的横坐标为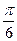 .(1)求
.(1)求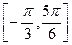 上的最小值为
上的最小值为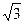 ,求a的值.
,求a的值.
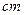 ,AD=12
,AD=12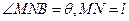 。
。
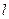 表示成
表示成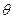 的函数;
的函数;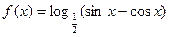 (1)求f(x)的定义域;(2)判断f(x)的奇偶性。
(1)求f(x)的定义域;(2)判断f(x)的奇偶性。 ,
, 的表达式是( )
的表达式是( )


