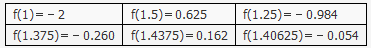题目内容
某同学准备用反证法证明如下问题:函数f(x)在[0,1]上有意义,且f(0)=f(1),如果对于不同的x1,x2∈[0,1]都有|f(x1)-f(x2)|<|x1-x2|,求证:|f(x1)-f(x2)|<,那么它的假设应该是
- A.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|<|x1-x2| 则|f(x1)-f(x2)|≥”
- B.“对于不同的x1,x2∈[0,1],都得|f(x1)-f(x2)|> |x1-x2| 则|f(x1)-f(x2)|≥”
- C.“?x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥”
- D.“?x1,x2∈[0,1],使得当|f(x1)-f(x2)|>|x1-x2|时有|f(x1)-f(x2)|≥”
C
由全称命题的否定是特称命题得:“对于不同的x1,x2∈[0,1]都有当|f(x1)-f(x2)|<|x1-x2| 时由|f(x1)-f(x2)|<”,否定为“?x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥”,故选C
由全称命题的否定是特称命题得:“对于不同的x1,x2∈[0,1]都有当|f(x1)-f(x2)|<|x1-x2| 时由|f(x1)-f(x2)|<”,否定为“?x1,x2∈[0,1],使得当|f(x1)-f(x2)|<|x1-x2| 时有|f(x1)-f(x2)|≥”,故选C

练习册系列答案
相关题目
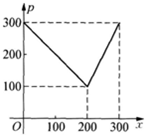 根据历年市场行情得知,从2月1日起的300天内,某种蔬菜的市场售价p与上市时间x的关系图是一条折线(如图),写出这种蔬菜的市场售价与时间的函数解析式p=p(x).
根据历年市场行情得知,从2月1日起的300天内,某种蔬菜的市场售价p与上市时间x的关系图是一条折线(如图),写出这种蔬菜的市场售价与时间的函数解析式p=p(x).