题目内容
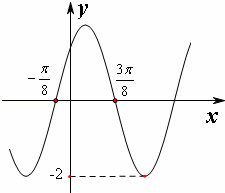
已知函数f(x)=Asin(ωx+ϕ),(A>0,ω>0,0≤ϕ≤π)的部分图象如图所示,则y=f(x)的解析式是f(x)= .
2sin(2x+ )考点: 由y=Asin(ωx+φ)的部分图象确定其解析式.
)考点: 由y=Asin(ωx+φ)的部分图象确定其解析式.
专题: 三角函数的图像与性质.
分析: 首先,根据所给函数的部分图象,得到振幅A=2,然后,根据周期得到ω的值,再将图象上的一个点代人,从而确定其解析式.
解答: 解:根据图象,得
A=2,
又∵ T=
T= =
= ,
,
∴T=π,
∴ω=2,
将点(﹣ ,0)代人,得
,0)代人,得
2sin(2x+ϕ)=0,
∵0≤ϕ≤π,
∴ϕ= ,
,
∴f(x)=2sin(2x+ ),
),
故答案为:2sin(2x+ )
)

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
某体育用品商场经营一批每件进价为40元的运动服,先做了市场调查,得到数据如下表:
| 销售单价x(元) | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y(件) | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据,解答下列问题:
⑴ 建立一个恰当的函数模型,使它能较好地反映销售量y(件)与销售单价x(元)之间的函数关系,并写出这个函数模型的解析式 ;
;
⑵ 试求销售利润z(元)与销售单价x(元)之间的函数关系式(销售利润 = 总销售收入 - 总进价成本)并求价格为多少利润最大?
 ,集合
,集合 ,则
,则 .
. 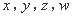 ,如果
,如果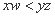 ,那么称
,那么称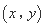 是
是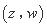 的“下位序对”.
的“下位序对”.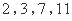 ,试求
,试求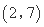 的“下位序对”;
的“下位序对”;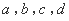 均为正数,且
均为正数,且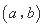 是
是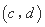 的“下位序对”,试判断
的“下位序对”,试判断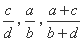 之间的大小关系;
之间的大小关系;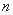 满足条件:对集合
满足条件:对集合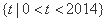 内的每个
内的每个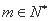 ,总存在
,总存在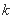
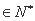 ,使得
,使得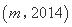 是
是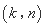 的“下位序对”,且
的“下位序对”,且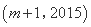 的“下位序对”.求正整数
的“下位序对”.求正整数 ,
, π<α<2π,则sinα=
π<α<2π,则sinα= 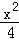 ﹣
﹣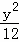 =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( )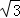 B. 2 C.
B. 2 C.  B.
B.  C.
C.  D.
D. 
 中,
中, 则________
则________ 与y=
与y= (a>0且a¹1),两者的图像相交于点P
(a>0且a¹1),两者的图像相交于点P ,如果x0³2,那么a的取值范围是_____________
,如果x0³2,那么a的取值范围是_____________