题目内容
对于四个正数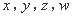 ,如果
,如果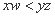 ,那么称
,那么称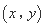 是
是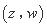 的“下位序对”.
的“下位序对”.
(1)对于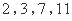 ,试求
,试求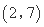 的“下位序对”;
的“下位序对”;
(2)设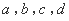 均为正数,且
均为正数,且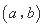 是
是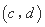 的“下位序对”,试判断
的“下位序对”,试判断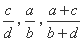 之间的大小关系;
之间的大小关系;
(3)设正整数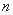 满足条件:对集合
满足条件:对集合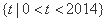 内的每个
内的每个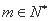 ,总存在
,总存在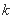
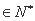 ,使得
,使得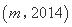 是
是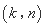 的“下位序对”,且
的“下位序对”,且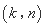 是
是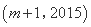 的“下位序对”.求正整数
的“下位序对”.求正整数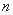 的最小值.
的最小值.
解:(1) ,
,
 的下位序对是
的下位序对是 .
.
(2)
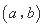 是
是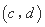 的“下位序对”,
的“下位序对”,
 ,
,
注意到 ,故
,故 ,即
,即 ,所以
,所以 ;
;
同理 . 综上所述,
. 综上所述, . (3)依题意,得
. (3)依题意,得 ,
,
注意到 ,
,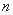 ,
,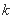 均为正整数,故
均为正整数,故 ,
,
于是 ,可得
,可得 ,该式对集合
,该式对集合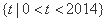 的每个正整数
的每个正整数 都成立,故
都成立,故 .
.
注意到 ,据(2)可得
,据(2)可得 ,
,
即 ,于是对
,于是对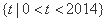 内的每个
内的每个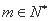 ,总存在
,总存在
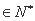 ,使得
,使得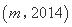 是
是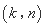 的“下位序对”,且
的“下位序对”,且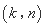 是
是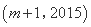 的“下位序对”,因此,正整数
的“下位序对”,因此,正整数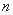 的最小值为
的最小值为 .
.

练习册系列答案
相关题目
 是边长为
是边长为 的正三角形,俯视图为正六边形,则侧视图的面积为( )
的正三角形,俯视图为正六边形,则侧视图的面积为( )
 B .
B .
 D.
D. 
 在区间
在区间 上恰有一个零点,则实数
上恰有一个零点,则实数 的取值范围是_____.
的取值范围是_____. (
( )的解集为
)的解集为 ,则
,则 .
. ,
, 为不超过实数
为不超过实数 的最大整数,若函数
的最大整数,若函数 存在最大值,
存在最大值,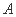 )
) (
(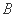 )
) (
(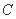 )
) (
(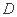 )
)
 ,B=
,B= ,若BA=
,若BA= ,则x=
,则x= 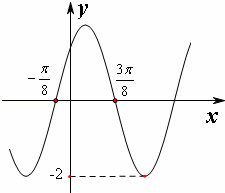
 的直线交抛物线于点P2,再过P2作斜率为
的直线交抛物线于点P2,再过P2作斜率为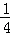 的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为
的直线交抛物线于点P3,﹣2<x<4,如此继续.一般地,过点3<x<5作斜率为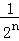 的直线交抛物线于点Pn+1,设点Pn(xn,yn).
的直线交抛物线于点Pn+1,设点Pn(xn,yn).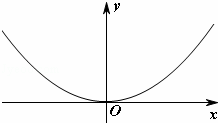
 ABC的三个内角,
ABC的三个内角, (1)若
(1)若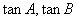 是方程
是方程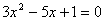 的两个实数根,判断
的两个实数根,判断