Question

自点A(－3，3)发出的光线l射到x轴上，被x轴反射，反射光线所在的直线与圆C：x²＋y²－4x－4y＋7＝0相切．求：

(1) 光线l和反射光线所在的直线方程；

(2) 光线自A到切点所经过的路程．

Answer 1

解：根据对称关系，首先求出点A的对称点A′的坐标为，其次设过A′的圆C的切线方程为

y＝k－3.

根据d＝r，即求出圆C的切线的斜率为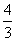k＝或k＝，

进一步求出反射光线所在的直线的方程为

4x－3y＋3＝0或3x－4y－3＝0.

最后根据入射光与反射光关于x轴对称，求出入射光所在直线方程为4x＋3y＋3＝0或3x＋4y－3＝0.

光路的距离为，可由勾股定理求得

＝－＝7.