题目内容
已知圆C：(x－1)2＋(y－2)2＝25，直线l：(2m＋1)x＋(m＋1)y－7m－4＝0(m∈R)．
(1) 求证：不论m取什么实数，直线l与圆C恒交于两点；
(2) 求直线被圆C截得的弦长最小时直线l的方程．
(1) 证明：直线l的方程整理得(x＋y－4)＋m(2x＋y－7)＝0，∵ m∈R，∴
也就是直线l恒过定点A(3，1)．由于|AC|＝
<5(半径)，∴ 点A(3，1)在圆C内，故直线l与圆C恒交于两点．
(2) 解：弦长最小时，直线l⊥AC，而kAC＝－
，故此时直线l的方程为2x－y－5＝0.
练习册系列答案
备战中考寒假系列答案
相关题目
，
，那么命题
为（ ） 
B．
D．
中，角
成等差数列，
也成等差数列，试判断这个三角形的形状；
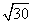PO？若存在，指出有几个这样的点；若不存在，请说明理由；
= 。
上满足
的
的值有 个