Question

【题目】设全集.

（1）解关于的不等式；

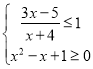（2）记为（1）中不等式的解集，为不等式组的整数解集，若恰有三个元素，求的取值范围.

Answer 1

【答案】（1）见解析（2）

【解析】

（1）通过讨论a的取值范围，求出不等式的解集即可.

（2）解不等式组求得集合B，通过讨论a的范围求出A的补集，再根据恰有三个元素，建立不等式求解.

（1）因为，

所以，

当 即 时，解集为R，

当 即 时，解集为 ，

当 即 时，或，

所以或，

所以解集为 或.

综上： 时，解集为R；

时，解集为 ；

时，解集为 或.

（2）因为，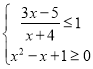

所以，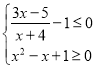

所以，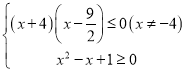

解得 .

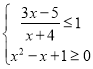因为为不等式组的整数解集，

所以 ，

当 时， 不满足恰有三个元素.

当 时，不满足恰有三个元素.

当 时， ， ，

因为恰有三个元素，

所以 ，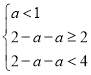

解得 .

综上：的取值范围是.