题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为圆
,右焦点为圆![]() 的圆心,且圆
的圆心,且圆![]() 截
截![]() 轴所得弦长为4.
轴所得弦长为4.
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 都只有一个公共点,记直线
都只有一个公共点,记直线![]() 与圆
与圆![]() 的公共点为
的公共点为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1) 椭圆![]() 的方程为
的方程为![]() ;圆
;圆![]() 的方程为
的方程为![]() . (2)
. (2) ![]() 或
或![]() .
.
【解析】
(1)由椭圆的离心率为![]() ,右焦点为圆C2:(x﹣1)2+y2=r2的圆心,列出方程组,求出a,b,c,由此能求出椭圆
,右焦点为圆C2:(x﹣1)2+y2=r2的圆心,列出方程组,求出a,b,c,由此能求出椭圆![]() 的方程;由圆
的方程;由圆![]() 截y轴所得弦长为4,得
截y轴所得弦长为4,得![]() =22+12=5,由此能求出圆
=22+12=5,由此能求出圆![]() 的方程.(2)设直线l的方程为y=kx+m,推导出4k2﹣m2=2km﹣5,由
的方程.(2)设直线l的方程为y=kx+m,推导出4k2﹣m2=2km﹣5,由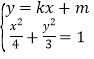 ,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、直线方程、圆、椭圆性质,结合已知条件能求出直线l与圆
,得(3+4k2)x2+8kmx+4m2﹣12=0,由此利用根的判别式、直线方程、圆、椭圆性质,结合已知条件能求出直线l与圆![]() 的公共点A的坐标.
的公共点A的坐标.
(1)由题意知:![]() 解得
解得![]()
又![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
因为圆![]() 截
截![]() 轴所得弦长为4,所以
轴所得弦长为4,所以![]() ,
,
所以圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,则
,则
![]() ,
,
即![]() ①
①
由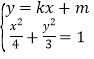 得
得![]() ,
,
因为直线![]() 与曲线
与曲线![]() 只有一个公共点,所以
只有一个公共点,所以
![]() ,
,
化简,得 ![]() ②
②
①②联立,解得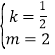 或
或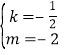
由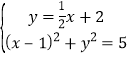 解得
解得![]() ,
,
由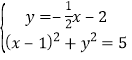 解得
解得![]() ,
,
故直线![]() 与圆
与圆![]() 的公共点
的公共点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目



