题目内容
【题目】(本小题满分12分)
如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】.证明:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………6分
………………………6分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………8分
.…………………………8分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……9分
所成的锐二面角的平面角.……9分
在![]() 中,
中,![]() ,即
,即![]() .……………10分
.……………10分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………12分
.…………12分
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立空间直角坐标系![]() ,如图.
,如图.
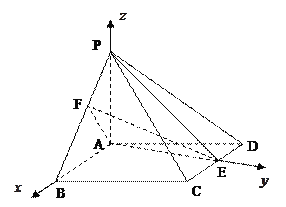
因为![]() ,
,![]() ,∴
,∴![]() 、
、![]() 、
、![]() 、
、![]() 6分
6分
则![]() ,
,![]() ,
,![]() .………7分
.………7分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………8分
.……………………8分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则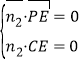 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………10分
. …………………10分
∴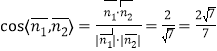 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……………12分
.……………12分
【解析】
试题分析:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………7分
………………………7分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………9分
.…………………………9分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……10分
所成的锐二面角的平面角.……10分
在![]() 中,
中,![]() ,即
,即![]() .……………11分
.……………11分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………14分
.…………14分
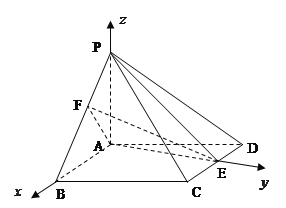
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,如图所示.因为
,如图所示.因为![]() ,
,![]() ,所以,
,所以,
![]() 、
、![]() 、
、![]() 、
、![]() ,…………7分
,…………7分
则![]() ,
,![]() ,
,![]() .………8分
.………8分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………9分
.……………………9分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则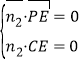 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………11分
. …………………11分
∴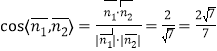 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……14分
.……14分

 字词句段篇系列答案
字词句段篇系列答案