题目内容
函数y=ax+logax(a>0,a≠1)零点的个数为________.
1
分析:由于此函数是由两个单调性相同的函数的和故,其单调性已知,再由函数零点存在的定理求出其零点的个数
解答:∵当a>1时,函数y=ax+logax(a>0,a≠1)是增函数,当当a<1时,函数y=ax+logax(a>0,a≠1)是减函数,
∴函数y=ax+logax(a>0,a≠1)是一个单调函数
故此函数至多有一个零点
又当a>1时,自变量接近0函数值接近负无穷大,当自变量接近于正无穷大时,函数值也趋向于正无穷大
当a<时,自变量接近0函数值接近正无穷大,当自变量接近于正无穷大时,函数值趋向于负无穷大
故此函数必有一个零点
故答案为1
点评:本题考查函数的零点,此类函数零点个数的判断,研究出其单调性及函数值的最值很关键,由于本题中函数是一个抽象函数,其底数范围对函数的单调性有影响,故采取了分类讨论的方法研究函数零点的个数
分析:由于此函数是由两个单调性相同的函数的和故,其单调性已知,再由函数零点存在的定理求出其零点的个数
解答:∵当a>1时,函数y=ax+logax(a>0,a≠1)是增函数,当当a<1时,函数y=ax+logax(a>0,a≠1)是减函数,
∴函数y=ax+logax(a>0,a≠1)是一个单调函数
故此函数至多有一个零点
又当a>1时,自变量接近0函数值接近负无穷大,当自变量接近于正无穷大时,函数值也趋向于正无穷大
当a<时,自变量接近0函数值接近正无穷大,当自变量接近于正无穷大时,函数值趋向于负无穷大
故此函数必有一个零点
故答案为1
点评:本题考查函数的零点,此类函数零点个数的判断,研究出其单调性及函数值的最值很关键,由于本题中函数是一个抽象函数,其底数范围对函数的单调性有影响,故采取了分类讨论的方法研究函数零点的个数

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数y=f(x)是函数y=ax-a(a>0,且a≠1)的反函数,且f(
)=1,则函数y=( )
| 1 |
| 2 |
| A、log2x | ||
B、
| ||
C、log
| ||
| D、2x-2 |
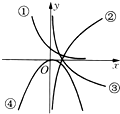 如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是( )
如图给出了函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2的图象,则与函数y=ax,y=logax,y=log(a+1)x,y=(a-1)x2依次对应的图象是( )