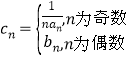题目内容
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;、
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
【答案】
(1)解:(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
∴[(n+1)an+1﹣nan](an+1+an)=0,∵an+1+an>0,
∴(n+1)an+1﹣nan=0,即 ![]() =
= ![]() .
.
∴an= ![]() …
… ![]() =
= ![]() …
… ![]() 1=
1= ![]() .
.
(2)解:证明:bn=a2n﹣1a2n+1= ![]() =
= ![]() .
.
数列{bn}的前n项和为Tn= ![]() +…+
+…+ ![]()
= ![]() .
.
即Tn< ![]() .
.
【解析】(1)利用分解因式可得(n+1)an+1﹣nan=0,再变形,利用累乘法可得{an}的通项公式;(2)利用裂项法可得数列{bn}的前n项和为Tn,进而可证Tn<![]() .
.
【考点精析】利用数列的前n项和和数列的通项公式对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系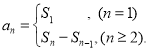 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

练习册系列答案
相关题目