题目内容
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点， |
| AE |
|
| AC |
分析：本题考查的知识点是与圆有关的比例线段，由于点F在直径AB上，不能直接应用切割线定理或相交弦定理，考虑构造相似形求解．连接OC后，易证明△POC∽△PDF，然后根据相似三角形的性质，结合AB=2BP=4即可得到答案．
解答：
解：连接OC，OD，OE，
由同弧对应的圆周角与圆心角之间的关系
结合题中条件
=
可得∠CDE=∠AOC，
又∠CDE=∠P+∠PFD，∠AOC=∠P+∠C，
从而∠PFD=∠C，故△PFD∽△PCO，
∴
=
，
由割线定理知PC•PD=PA•PB=12，
故PF=
=
=3．---（12分）
解：连接OC，OD，OE，由同弧对应的圆周角与圆心角之间的关系
结合题中条件
|
| AE |
|
| AC |
又∠CDE=∠P+∠PFD，∠AOC=∠P+∠C，
从而∠PFD=∠C，故△PFD∽△PCO，
∴
| PF |
| PC |
| PD |
| PO |
由割线定理知PC•PD=PA•PB=12，
故PF=
| PC•PD |
| PO |
| 12 |
| 4 |
点评：本题是考查同学们推理能力、逻辑思维能力的好资料，题目以证明题为主，特别是一些定理的证明和用多个定理证明一个问题的题目，我们注意熟练掌握：1．射影定理的内容及其证明； 2．圆周角与弦切角定理的内容及其证明；3．圆幂定理的内容及其证明；4．圆内接四边形的性质与判定．
练习册系列答案
相关题目
21、如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．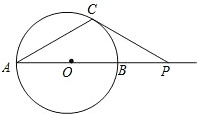
如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过p点作⊙O的切线，切点为C，连接AC，若∠CPA=30°，PC=
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）