��Ŀ����
 ������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣���
������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣���A���躯��f��x��=|2x+1|-|x-4|����ʽf��x����2�Ľ⼯Ϊ
{x|x��-7��x��
}
| 5 |
| 3 |
{x|x��-7��x��
}
��| 5 |
| 3 |
B��������ϵ���������ѡ���⣩����C��
|
��=-4cos��
��=-4cos��
��C��������֤��ѡ��ѡ���⣩ ��ͼ����O��ֱ��AB���ӳ�������CD���ӳ����ཻ�ڵ�P��EΪ��O��һ�㣬��AE=��AC��DE��AB��F����AB=2BP=4����PF=
3
3
��������A��ͨ����x��������ȥ������ֵ���ż�����÷ֶκ���f��x���ı���ʽ���Ӷ���|��ò���ʽf��x����2�Ľ⼯��
B������������Ե�O��0��0��Ϊ���㣬x������Ϊ���Ὠ��������ϵ����ͼ�Σ��Ӷ��õ������ߵļ����귽�̣�
C�����ڵ�F��ֱ��AB�ϣ��ɹ��������Σ����ø��߶���ת����⣮
B������������Ե�O��0��0��Ϊ���㣬x������Ϊ���Ὠ��������ϵ����ͼ�Σ��Ӷ��õ������ߵļ����귽�̣�
C�����ڵ�F��ֱ��AB�ϣ��ɹ��������Σ����ø��߶���ת����⣮
����⣺����A����f��x��=|2x+1|-|x-4|=
��
�൱x��-
ʱ��f��x����2?-x-5��2��
��x��-7��
��-
��x��4ʱ��f��x����2?3x-3��2��
��
��x��4��
��x��4ʱ��f��x����2?x+5��2��
��x��4��
��������������ʽf��x����2�Ľ⼯Ϊ{x|x��-7��x��
}��
����B���ɲ�������
������ͨ����Ϊ����x+2��2+y2=4��
���Ե�O��0��0��Ϊ���㣬x������Ϊ���Ὠ��������ϵ��
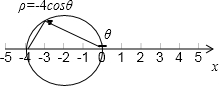
������ߵļ����귽���Ǧ�=4cos����-�ȣ�=-4cos�ȣ�
����C������OC��
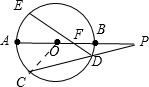
�ߡ�AOC�Ķ���=��AC�Ķ�������EDC�Ķ���=
��EC�Ķ���=��AC�Ķ���
���AOC=��EDC��
���POC=��PDF��
���POC�ס�PDF
��
=
��
��PF=
=
=2��
=3��
�ʴ�Ϊ��A��{x|x��-7��x��
}��B����=-4cos�ȣ�C��3��
|
�൱x��-
| 1 |
| 2 |
��x��-7��
��-
| 1 |
| 2 |
��
| 5 |
| 3 |
��x��4ʱ��f��x����2?x+5��2��
��x��4��
��������������ʽf��x����2�Ľ⼯Ϊ{x|x��-7��x��
| 5 |
| 3 |
����B���ɲ�������
|
���Ե�O��0��0��Ϊ���㣬x������Ϊ���Ὠ��������ϵ��

������ߵļ����귽���Ǧ�=4cos����-�ȣ�=-4cos�ȣ�
����C������OC��

�ߡ�AOC�Ķ���=��AC�Ķ�������EDC�Ķ���=
| 1 |
| 2 |
���AOC=��EDC��
���POC=��PDF��
���POC�ס�PDF
��
| PD |
| PO |
| PF |
| PC |
��PF=
| PC��PD |
| PO |
| PB��PA |
| PO |
| 6 |
| 4 |
�ʴ�Ϊ��A��{x|x��-7��x��
| 5 |
| 3 |
����������A�������ֵ����ʽ�Ľⷨ��ͨ����x��������ȥ������ֵ�����ǹؼ���B��������ߵļ����귽�̣�����������ת��Ϊ�����귽���ǹؼ���C���鼸��֤��������������������������ǹؼ��������и��߶���ת�����ѵ㣬�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
 ������ע�⣺����������������ѡһ����������������������ĵ�һ�����֣�
������ע�⣺����������������ѡһ����������������������ĵ�һ�����֣� ����ѡһ������ע�⣺����������������ѡһ����������������������ĵ�һ�����֣�
����ѡһ������ע�⣺����������������ѡһ����������������������ĵ�һ�����֣� ������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣�
������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣� ������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣�
������ע�⣺����������������ѡһ����������������������ĵ�һ�����ļǷ֣�