题目内容
设函数f(x)=sin( x+
x+ )-2sin2
)-2sin2 x.
x.
(1)求函数f(x)的最小正周期;
(2)若函数y=g(x)的图象与函数y=f(x)的图象关于原点对称,求S=g(1)+g(2)+…+g(2012)的值.
解:(1)∵函数f(x)=sin( x+
x+ )-2sin2
)-2sin2 x=
x= sin
sin x+
x+ cos
cos x-2•
x-2•
= (
( sin
sin x+
x+ cos
cos x)-1=
x)-1= sin(
sin( x+
x+ )-1,
)-1,
故函数f(x)的最小正周期T= =4.
=4.
(2)∵函数y=g(x)的图象与函数y=f(x)的图象关于原点对称,在函数y=g(x)的图象上任取一点
(x,g(x)),则它关于原点的对称点(-x,-g(x))在函数y=f(x)的图象上,
即点(-x,-g(x))的坐标满足函数y=f(x)的解析式,故有-g(x)= sin(-
sin(- x+
x+ )-1=-
)-1=- sin(
sin( x-
x- )-1,
)-1,
∴g(x)= sin(
sin( x-
x- )+1,故函数g(x)的周期为4.
)+1,故函数g(x)的周期为4.
∵g(1)= sin(
sin( -
- )+1=
)+1= +1,g(2)=
+1,g(2)= sin(
sin( ×2-
×2- )+1=
)+1= +1,g(3)=
+1,g(3)= sin(
sin( ×3-
×3- )+1=1-
)+1=1- ,
,
g(4)= sin(
sin( ×4-
×4- )+1=1-
)+1=1- ,∴g(1)+g(2)+g(3)+g(4)=4.
,∴g(1)+g(2)+g(3)+g(4)=4.
S=g(1)+g(2)+…+g(2012)=503(g(1)+g(2)+g(3)+g(4))=503×4=2012.
分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为 sin(
sin( x+
x+ )-1,由此求得f(x)的最小正周期.
)-1,由此求得f(x)的最小正周期.
(2)在函数y=g(x)的图象上任取一点(x,g(x)),则它关于原点的对称点(-x,-g(x))在函数y=f(x)的图象上,由此求得 g(x)= sin(
sin( x-
x- )+1,由此求得
)+1,由此求得
函数g(x)的周期为4,求出g(1)+g(2)+g(3)+g(4)的值,即可求得S=g(1)+g(2)+…+g(2012)的值.
点评:本题主要考查三角函数的恒等变换及化简求值,利用函数的周期性求函数值,属于中档题.
 x+
x+ )-2sin2
)-2sin2 x=
x= sin
sin x+
x+ cos
cos x-2•
x-2•
=
 (
( sin
sin x+
x+ cos
cos x)-1=
x)-1= sin(
sin( x+
x+ )-1,
)-1,故函数f(x)的最小正周期T=
 =4.
=4.(2)∵函数y=g(x)的图象与函数y=f(x)的图象关于原点对称,在函数y=g(x)的图象上任取一点
(x,g(x)),则它关于原点的对称点(-x,-g(x))在函数y=f(x)的图象上,
即点(-x,-g(x))的坐标满足函数y=f(x)的解析式,故有-g(x)=
 sin(-
sin(- x+
x+ )-1=-
)-1=- sin(
sin( x-
x- )-1,
)-1,∴g(x)=
 sin(
sin( x-
x- )+1,故函数g(x)的周期为4.
)+1,故函数g(x)的周期为4.∵g(1)=
 sin(
sin( -
- )+1=
)+1= +1,g(2)=
+1,g(2)= sin(
sin( ×2-
×2- )+1=
)+1= +1,g(3)=
+1,g(3)= sin(
sin( ×3-
×3- )+1=1-
)+1=1- ,
,g(4)=
 sin(
sin( ×4-
×4- )+1=1-
)+1=1- ,∴g(1)+g(2)+g(3)+g(4)=4.
,∴g(1)+g(2)+g(3)+g(4)=4.S=g(1)+g(2)+…+g(2012)=503(g(1)+g(2)+g(3)+g(4))=503×4=2012.
分析:(1)利用三角函数的恒等变换化简函数f(x)的解析式为
 sin(
sin( x+
x+ )-1,由此求得f(x)的最小正周期.
)-1,由此求得f(x)的最小正周期.(2)在函数y=g(x)的图象上任取一点(x,g(x)),则它关于原点的对称点(-x,-g(x))在函数y=f(x)的图象上,由此求得 g(x)=
 sin(
sin( x-
x- )+1,由此求得
)+1,由此求得函数g(x)的周期为4,求出g(1)+g(2)+g(3)+g(4)的值,即可求得S=g(1)+g(2)+…+g(2012)的值.
点评:本题主要考查三角函数的恒等变换及化简求值,利用函数的周期性求函数值,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
设函数f(x)=sin(2x+
),则下列结论正确的是( )
| π |
| 6 |
A、f(x)的图象关于直线x=
| ||
B、f(x)的图象关于点(
| ||
C、f(x)的最小正周期为π,且在[0,
| ||
D、把f(x)的图象向右平移
|
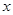 )=sin(2
)=sin(2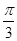 ),则下列结论正确的是(
)
),则下列结论正确的是(
)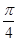 ,0)对称
,0)对称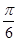 ]上为增函数
]上为增函数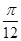 个单位,得到一个偶函数的图像
个单位,得到一个偶函数的图像