题目内容
设函数f(x)=sin2x-sin(2x-
).
(1)求函数f(x)的最大值和最小值;
(2)△ABC的内角A,B,C的对边分别为a,b,c,c=3,f(
)=
,若sinB=2sinA,求△ABC的面积.
| π |
| 2 |
(1)求函数f(x)的最大值和最小值;
(2)△ABC的内角A,B,C的对边分别为a,b,c,c=3,f(
| C |
| 2 |
| 1 |
| 4 |
分析:(1)利用二倍角的余弦函数以及诱导公式,化简函数的表达式,然后求出函数的最值.
(2)利用f(
)=
,结合(1)求出C的大小,利用正弦定理求出a,b的方程,通过余弦定理联立方程组,求出a,即可求解三角形的面积.
(2)利用f(
| C |
| 2 |
| 1 |
| 4 |
解答:解:(1)f(x)=sin2x-sin(2x-
)
=
+cos2x=
cos2x+
∴当cos2x=1时,函数取得最大值1;
当cos2x=-1时,函数取得最小值0.
(2)∵f(
)=
,∴
cosC+
=
,即cosC=-
.
又∵C∈(0,π),
∴C=
.
∵sinB=2sinA,
∴b=2a.
∵c=3,
∴9=a2+4a2-2a×2a×cos
∴a2=
∴S△ABC=
absinC=a2sinC=
.
△ABC的面积:
.
| π |
| 2 |
=
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当cos2x=1时,函数取得最大值1;
当cos2x=-1时,函数取得最小值0.
(2)∵f(
| C |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
又∵C∈(0,π),
∴C=
| 2π |
| 3 |
∵sinB=2sinA,
∴b=2a.
∵c=3,
∴9=a2+4a2-2a×2a×cos
| 2π |
| 3 |
∴a2=
| 9 |
| 7 |
∴S△ABC=
| 1 |
| 2 |
9
| ||
| 14 |
△ABC的面积:
9
| ||
| 14 |
点评:本题考查二倍角的三角函数,余弦定理、正弦定理以及三角形的面积的求法,考查计算能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 )-cos2(x+
)-cos2(x+ )(x∈R),则函数f(x)是( )
)(x∈R),则函数f(x)是( ) 的奇函数
的奇函数 的偶函数
的偶函数 sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
sinωx•cosωx-cos2ωx+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈( ,1).
,1). ,求函数f(x)的值域.
,求函数f(x)的值域.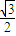 -
- sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为
sin2ωx-sinωxcosωx(ω>0),且y=f(x)的图象的一个对称中心到最近的对称轴的距离为 ,
, ]上的最大值和最小值.
]上的最大值和最小值.