题目内容
设x1,x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a＞0)的两个极值点.(1)若x1=-1，x2=2,求f(x)的解析式；
(2)若|x1|+|x2|=
，求b的最大值；
(3)若x1＜x＜x2，且x2=a，函数g(x)=f′(x)-a(x-x1)，求证：|g(x)|≤
a(3a+2)2.
答案：f′(x)=3ax2+2bx-a2(a＞0).1分
(1)解：∵x1=-1,x2=2是函数f(x)的两个极值点，∴f′(-1)=0,f′(2)=0.
∴3a-2b-a2=0,12a+4b-a2=0，解得a=6,b=-9.
∴f(x)=6x3-9x2-36x.4分
(2)解：∵x1,x2是f(x)的两个极值点，
∴f′(x1)=f′(x2)=0.
∴x1,x2是方程3ax2+2bx-a2=0的两根.
∵Δ=4b2+12a3，
∴Δ＞0对一切a＞0,b∈R恒成立,
x1+x2=，x1·x2=.
∵a＞0,∴x1·x2＜0.
∴|x1|+|x2|=|x1-x2|=
.
由|x1|+|x2|=
,得
，
∴b2=3a2(6-a).
∵b2≥0，∴3a2(6-a)≥0，∴0＜a≤6.
令h(a)=3a2(6-a)，则h′(a)=-9a2+36a.
0＜a＜4时，h′(a)＞0,∴h(a)在(0，4)内是增函数；
4＜a＜6时，h′(a)＜0,∴h(a)在(4，6)内是减函数.
∴a=4时，h(a)有极大值为96，∴h(a)在(0,6］上的最大值是96，
∴b的最大值是
.
(3)证法一：∵x1,x2是方程f′(x)=0的两根，
∴f′(x)=3a(x-x1)(x-x2)，
∴|g(x)|=3a|x-x1|·|x-x2
|≤3a(
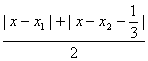)2.
∵x1＜x＜x2，∴x-x1＞0,x-x2＜0，
∴|g(x)|≤
［(x-x1)-(x-x2
)］2=
(x2-x1+
)2.
∵x1·x2=
，x2=a,∴x1=
.
∴|g(x)|≤
·(a+
)2
=
a(3a+2)2.
证法二：∵x1,x2是方程f′(x)=0的两根，
∴f′(x)=3a(x-x1)(x-x2)，10分
∵x1·x2=
，x2=a,∴x1=
.
∴|g(x)|=|3a(x+
)(x-a)-a(x+
)|=|a(x+
)［3(x-a)-1］|.∵x1＜x＜x2，
∴|g(x)|=a(x+
)(-3x+3a+1).
=-3a(x+
)(x
)
=-3a(x
)2+
+a2+
a≤
+a2+
.
快乐暑假暑假能力自测中西书局系列答案
,
在(0,+∞)上是增函数；
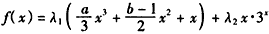（a，b∈R，a＞0）。