题目内容
【题目】过直线![]() 上的点
上的点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,切点分别为
,切点分别为![]() ,联结
,联结![]() .
.
(1)当点![]() 在直线
在直线![]() 上运动时,证明:直线
上运动时,证明:直线![]() 恒过定点
恒过定点![]() ;
;
(2)当![]() 时,定点
时,定点![]() 平分线段
平分线段![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
设![]() .则椭圆过点
.则椭圆过点![]() 的切线方程分别为
的切线方程分别为![]() .因为两切线都过点
.因为两切线都过点![]() ,所以,
,所以,![]() .
.
这表明点![]() 均在直线
均在直线![]() ①
①
上.由两点决定一条直线知,式①就是直线![]() 的方程,其中
的方程,其中![]() 满足直线
满足直线![]() 的方程.
的方程.
(1)当![]() 在直线
在直线![]() 上运动时,可理解为
上运动时,可理解为![]() 取遍一切实数,相应的
取遍一切实数,相应的![]() 为
为![]() .代
.代
入式①消去![]() 得
得![]() ②
②
对一切![]() 恒成立.
恒成立.
变形可得![]() 对一切
对一切![]() 恒成立.
恒成立.
则![]() .由此得直线
.由此得直线![]() 恒过定点
恒过定点![]() .
.
(2)当![]() 时,由式②知
时,由式②知![]() .解得
.解得![]() .
.
代入式②得![]() 的方程为
的方程为![]() ③
③
将此方程与椭圆方程联立,消去![]() 得
得![]() .
.
由此得![]() 截椭圆所得弦的中点横坐标恰好为点
截椭圆所得弦的中点横坐标恰好为点![]() 的横坐标,即
的横坐标,即![]() .
.
代入式③可得弦中点纵坐标恰好为点![]() 的纵坐标,即
的纵坐标,即![]() .
.
这就是说,点![]() 平分线段
平分线段![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: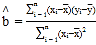 ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?