题目内容
【题目】在四面体ABCD中，
与
都是边长为8的正三角形，点O是线段BC的中点.
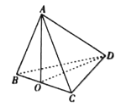
（1）证明：
.
（2）若
为锐角，且四面体ABCD的体积为
求侧面ACD的面积.
【答案】（1）证明见解析；（2）
.
【解析】
（1）通过正三角形的性质易得
，
，由线面垂直判定定理可得
平面AOD，最后由线垂直于某个面线将垂直于该面内所有直线即可得结果；
（2）过点D作
，垂足为E，易得平面
平面ABC，根据面面垂直性质定理可得
平面ABC，由四面体的体积可得
，接着算出
，根据三角形面积公式即可得结果.
（1）证明：
是正三角形，
.
∵
也是正三角形，
，且
平面AOD.
又
平面AOD，
.
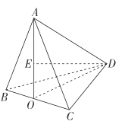
（2）过点D作，垂足为E.
∵平面ADO，且
平面ABC，
平面平面ABC
又平面
平面
，
平面ABC.
四面体ABCD的体积为
，
的面积
，
，
.
又
，
，
，
.
练习册系列答案
相关题目
【题目】为弘扬中华传统文化，学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查，小明同学阅读两类读物的阅读量统计如下：
小明阅读“经典名著”的阅读量
（单位：字）与时间t（单位：分钟）满足二次函数关系，部分数据如下表所示；
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量
（单位：字）与时间t（单位：分钟）满足如图1所示的关系.
（1）请分别写出函数
和
的解析式；
（2）在每天的一小时课外阅读活动中，小明如何分配“经典名著”和“古诗词”的阅读时间，使每天的阅读量最大，最大值是多少？
