题目内容
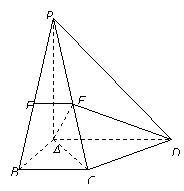
如图,在四棱 锥
锥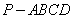 中,平面
中,平面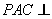 平面
平面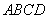 ,且
,且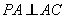 ,
, 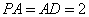 .四边形
.四边形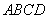 满足
满足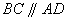 ,
,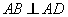 ,
,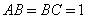 .
.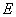 为侧棱
为侧棱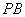 的中点,
的中点,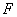 为侧棱
为侧棱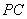 上的任意一点.
上的任意一点.
(Ⅰ)若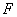 为
为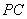 的中点,求证:
的中点,求证: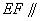 平面
平面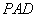 ;
;
(Ⅱ)求证:平面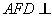 平面
平面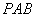 ;
;
(Ⅲ)是否存在点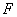 ,使得直线
,使得直线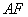 与平面
与平面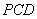 垂直?若存在,写出证明过程并求出线段
垂直?若存在,写出证明过程并求出线段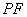 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 |
证明:(Ⅰ)因为 分别为侧棱
分别为侧棱 的中点,
的中点,
所以  .
.
 因为
因为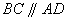 ,所以
,所以 .
.
而 平面
平面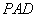 ,
, 平面
平面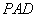 ,
,
所以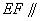 平面
平面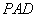 .
.
(Ⅱ)因为平面 平面
平面 ,
,
平面 平面
平面 ,且
,且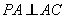 ,
, 平面
平面 .
.
所以 平面
平面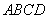 ,又
,又 平面
平面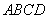 ,所以
,所以 .
.
又因为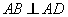 ,
, ,所以
,所以 平面
平面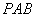 ,
,
而 平面
平面 ,
,
所以平面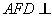 平面
平面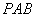 .…
.…
(Ⅲ)存在点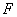 ,使得直线
,使得直线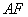 与平面
与平面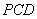 垂直.
垂直.
在棱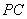 上显然存在点
上显然存在点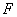 ,使得
,使得 .
.
由已知,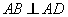 ,
,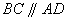 ,
,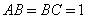 ,
, .
.
由平面几何知识可得  .
.
由(Ⅱ)知, 平面
平面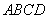 ,所以
,所以 ,
,
因为 ,所以
,所以 平面
平面 .
.
而 平面
平面 ,所以
,所以 .[来源:学科网]
.[来源:学科网]
又因为 ,所以
,所以 平面
平面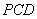 .
.
在 中,
中, ,
,
可求得, .
.
可见直线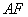 与平面
与平面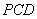 能够垂直,此时线段
能够垂直,此时线段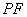 的长为
的长为 .
.

练习册系列答案
相关题目
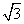 的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )
的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )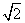 B.
B. 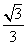 D.
D. 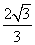
 .若
.若 ,使
,使 成立,则称
成立,则称 为函数
为函数 的一个“生成点”.函数
的一个“生成点”.函数 与圆
与圆 有两个不同的公共点,则实数
有两个不同的公共点,则实数 的取值范围是
的取值范围是 B.
B.
 D .
D . 
 中,
中,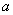 ,
, ,
, 分别为角
分别为角 ,
, ,
,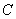 所对的边,且满足
所对的边,且满足 ,则
,则 ,
, ,则
,则
 .
. ,
, ,则
,则
 B.
B.  C.
C.  D.
D. 
 的右焦点为焦点,顶点在原点的抛物线的标准方程是 .
的右焦点为焦点,顶点在原点的抛物线的标准方程是 .  y+2=0被圆
y+2=0被圆 截得的弦长为_________。
截得的弦长为_________。 .
. 的单调区间;
的单调区间;  时,求函数
时,求函数 上的最小值.
上的最小值.