题目内容
已知抛物线C:x2=4y的焦点为F,过点K(0,-1)的直线l与C相交于A,B两点,点A关于y轴的对称点为D.
(1)证明:点F在直线BD上;
(2)设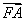 ·
·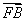 =
=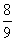 ,求∠DBK的平分线与y轴的交点坐标.
,求∠DBK的平分线与y轴的交点坐标.
解:(1)证明:设A(x1,y1),B(x2,y2),
D(-x1,y1),l的方程为y=kx-1,
由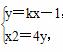 得x2-4kx+4=0,
得x2-4kx+4=0,
从而x1+x2=4k,x1x2=4.
直线BD的方程为y-y1=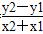 (x+x1),
(x+x1),
即y-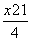 =
=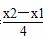 (x+x1),
(x+x1),
令x=0,得y=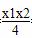 =1,所以点F在直线BD上.
=1,所以点F在直线BD上.
(2)因为FA―→·FB―→=(x1,y1-1)·(x2,y2-1)=x1x2+(y1-1)·(y2-1)=8-4k2,
故8-4k2=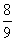 ,解得k=±
,解得k=±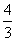 ,
,
所以l的方程为4x-3y-3=0,4x+3y+3=0.
又由(1)得x2-x1=±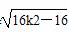 =±
=±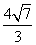 ,
,
故直线BD的斜率为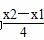 =±
=±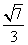 ,
,
因而直线BD的方程为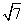 x-3y+3=0,
x-3y+3=0,
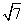 x+3y-3=0.
x+3y-3=0.
设∠DBK的平分线与y轴的交点为M(0,t),
则M(0,t)到l及BD的距离分别为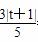 ,
,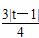 ,
,
由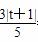 =
=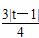 ,得t=
,得t=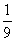 或t=9(舍去),
或t=9(舍去),
所以∠DBK的平分线与y轴的交点为
M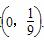 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
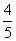 .
.
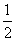 D.
D.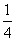
 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 ,那么cos A等于( )
,那么cos A等于( ) B.
B.  C.-
C.-
 的单调区间;
的单调区间; 有三个不同的解,求实数
有三个不同的解,求实数 的范围.
的范围.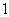 的等比数列
的等比数列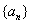 的首项
的首项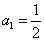 ,前
,前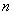 项和为
项和为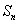 ,且
,且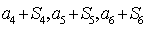 成等差数列.
成等差数列.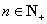 ,在
,在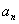 与
与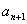 之间插入
之间插入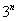 个数,使这
个数,使这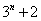 个数成等差数列,记插入的这
个数成等差数列,记插入的这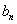 ,求数列
,求数列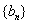 的前
的前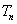 .
.