题目内容
在空间四边形ABCD中,E、F分别为AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( )
A.90° B. 60° C. 45° D. 30°
D
解析试题分析:解:如图所示:取AD的中点G,连接GE,GF
则GE∥CD,且GE= CD=2
CD=2
则∠FEG即为EF与CD所成的角
GF∥AB,且GF= AB=1
AB=1
又∵EF⊥AB,
∴EF⊥GF,
∴∠FEG=30°
故选D
考点:异面直线所成角

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设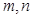 是不同的直线,
是不同的直线,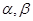 是不同的平面,下列命题中正确的是( )
是不同的平面,下列命题中正确的是( )
A.若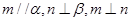 ,则 ,则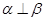 |
B.若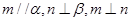 ,则 ,则 |
C.若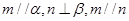 ,则 ,则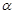 ⊥ ⊥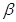 |
D.若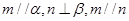 ,则 ,则 |
关于直线 及平面
及平面 ,下列命题中正确的是( )
,下列命题中正确的是( )
A. | B. |
C. | D. |
设 是两个不同的平面,
是两个不同的平面, 是一条直线,则下列命题正确的是( )
是一条直线,则下列命题正确的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
若空间三条直线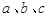 满足
满足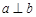 ,
,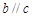 ,则直线
,则直线 与
与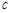 ( ).
( ).
| A.一定平行 | B.一定相交 | C.一定是异面直线 | D.一定垂直 |
已知平面 外不共线的三点
外不共线的三点 到
到 α的距离都相等,则正确的结论是( )
α的距离都相等,则正确的结论是( )
A.平面 必平行于 必平行于 |
B.平面 必与 必与 相交 相交 |
C.平面 必不垂直于 必不垂直于 |
D.存在△ 的一条中位线平行于 的一条中位线平行于 或在 或在 内 内 |
已知直线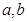 都在平面
都在平面 外, 则下列推断错误的是( )
外, 则下列推断错误的是( )
A. | B. |
C. | D. |
给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是 ( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
已知直线 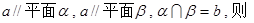
 与
与 ( )
( )
| A.相交 | B.平行 | C.异面 | D.共面或异面 |