题目内容
△ABC的三个内角分别是A,B,C,若sinC=2cosAsinB,则此△ABC的形状一定是
等腰三角形
等腰三角形
.分析:直接利用三角形的内角和已经两角和的正弦函数,化简然后的表达式,通过求解角的大小,即可判断三角形的形状.
解答:解:因为A+B+C=π,sinC=2cosAsinB,
所以sin(A+B)=2cosAsinB,
即sinAcosB+cosAsinB=2cosAsinB,
sinAcosB-cosAsinB=0,
所以sin(A-B)=0
因为A,B是三角形内角,所以A-B=0,
即A=B,三角形是等腰三角形.
故答案为:等腰三角形.
所以sin(A+B)=2cosAsinB,
即sinAcosB+cosAsinB=2cosAsinB,
sinAcosB-cosAsinB=0,
所以sin(A-B)=0
因为A,B是三角形内角,所以A-B=0,
即A=B,三角形是等腰三角形.
故答案为:等腰三角形.
点评:本题考查三角形的形状的判定,两角和与差的三角函数,三角函数值的求法,考查计算能力.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 与
与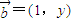 共线,且有函数y=f(x).
共线,且有函数y=f(x). ,边
,边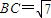 ,
,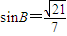 ,求AC的长.
,求AC的长. 与
与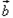 =(1,y)共线,且有函数y=f(x),
=(1,y)共线,且有函数y=f(x), ,边BC=
,边BC=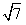 ,sinB=
,sinB=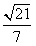 ,求AC的长。
,求AC的长。