МвДїДЪИЭ
ЎѕМвДїЎїЛжЧЕКЦ»ъµД·ўХ№Ј¬Ў°ОўРЕЎ±ЦрЅҐіЙОЄИЛГЗЦ§ё¶№єОпµДТ»ЦЦРОКЅ.Ді»ъ№№¶ФЎ°К№УГОўРЕЦ§ё¶Ў±µДМ¬¶ИЅшРРµчІйЈ¬Лж»ъійИЎБЛ50ИЛЈ¬ЛыГЗДкБдµДЖµКэ·ЦІјј°¶ФЎ°К№УГОўРЕЦ§ё¶Ў±ФЮіЙИЛКэИзПВ±н.
ДкБд ЈЁµҐО»ЈєЛкЈ© |
|
|
|
|
|
|
ЖµКэ | 5 | 10 | 15 | 10 | 5 | 5 |
ФЮіЙИЛКэ | 5 | 10 | 12 | 7 | 2 | 1 |
ЈЁўсЈ©ИфТФЎ°ДкБд45ЛкОЄ·ЦЅзµгЎ±Ј¬УЙТФЙПНіјЖКэѕЭНкіЙПВГж![]() БРБЄ±нЈ¬ІўЕР¶ПКЗ·сУР99%µД°СОХИПОЄЎ°К№УГОўРЕЦ§ё¶Ў±µДМ¬¶ИУлИЛµДДкБдУР№ШЈ»
БРБЄ±нЈ¬ІўЕР¶ПКЗ·сУР99%µД°СОХИПОЄЎ°К№УГОўРЕЦ§ё¶Ў±µДМ¬¶ИУлИЛµДДкБдУР№ШЈ»
ДкБдІ»µНУЪ45ЛкµДИЛКэ | ДкБдµНУЪ45ЛкµДИЛКэ | єПјЖ | |
ФЮіЙ | |||
І»ФЮіЙ | |||
єПјЖ |
ЈЁўтЈ©ИфґУДкБдФЪ![]() µД±»µчІйИЛЦР°ґХХФЮіЙУлІ»ФЮіЙ·ЦІгійСщЈ¬ійИЎ5ИЛЅшРРЧ·ЧЩµчІйЈ¬ФЪ5ИЛЦРійИЎ3ИЛЧцЧЁ·ГЈ¬Зу3ИЛЦРІ»ФЮіЙК№УГОўРЕЦ§ё¶µДИЛКэµД·ЦІјБРєНЖЪНыЦµ.
µД±»µчІйИЛЦР°ґХХФЮіЙУлІ»ФЮіЙ·ЦІгійСщЈ¬ійИЎ5ИЛЅшРРЧ·ЧЩµчІйЈ¬ФЪ5ИЛЦРійИЎ3ИЛЧцЧЁ·ГЈ¬Зу3ИЛЦРІ»ФЮіЙК№УГОўРЕЦ§ё¶µДИЛКэµД·ЦІјБРєНЖЪНыЦµ.
ІОїјКэѕЭЈє
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() .
.
Ўѕґр°ёЎїЈЁўсЈ©ПкјыЅвОцЈ»ЈЁўтЈ©ПкјыЅвОц.
ЎѕЅвОцЎї
ЈЁўсЈ©ёщѕЭЖµКэ·ЦІј±нІ№И«БРБЄ±нЈ¬ґъИ빫ʽїЙЗуµГ![]() Ј¬ґУ¶шїЙЦЄУР
Ј¬ґУ¶шїЙЦЄУР![]() µД°СОХЈ»ЈЁўтЈ©ёщѕЭ·ЦІгійСщµД·Ѕ·ЁїЙЦЄійИЎµД
µД°СОХЈ»ЈЁўтЈ©ёщѕЭ·ЦІгійСщµД·Ѕ·ЁїЙЦЄійИЎµД![]() ИЛЦРЈ¬Ц§іЦОўРЕЦ§ё¶
ИЛЦРЈ¬Ц§іЦОўРЕЦ§ё¶![]() ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶
ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶![]() ИЛЈ¬ёщѕЭі¬јёєО·ЦІјµДМШµгЗуµГ·ЦІјБРєНКэС§ЖЪНы.
ИЛЈ¬ёщѕЭі¬јёєО·ЦІјµДМШµгЗуµГ·ЦІјБРєНКэС§ЖЪНы.
ЈЁўсЈ©УЙЖµКэ·ЦІј±нµГ![]() БРБЄ±нИзПВЈє
БРБЄ±нИзПВЈє
ДкБдІ»µНУЪ45ЛкµДИЛКэ | ДкБдµНУЪ45ЛкµДИЛКэ | єПјЖ | |
ФЮіЙ |
|
|
|
І»ФЮіЙ |
|
| 13 |
єПјЖ |
|
|
|
![]()
![]() УР
УР![]() µД°СОХИПОЄЎ°К№УГОўРЕЅ»БчЎ±µДМ¬¶ИУлИЛµДДкБдУР№Ш
µД°СОХИПОЄЎ°К№УГОўРЕЅ»БчЎ±µДМ¬¶ИУлИЛµДДкБдУР№Ш
ЈЁўтЈ©ДкБдФЪ![]() ЦРЦ§іЦОўРЕЦ§ё¶
ЦРЦ§іЦОўРЕЦ§ё¶![]() ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶6ИЛ
ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶6ИЛ
УЙ·ЦІгійСщ·Ѕ·ЁїЙЦЄЈєійИЎµД![]() ИЛЦРЈ¬Ц§іЦОўРЕЦ§ё¶
ИЛЦРЈ¬Ц§іЦОўРЕЦ§ё¶![]() ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶
ИЛЈ¬І»Ц§іЦОўРЕЦ§ё¶![]() ИЛ
ИЛ
Йи![]() ИЛЦРІ»Ц§іЦОўРЕЦ§ё¶µДИЛКэОЄ
ИЛЦРІ»Ц§іЦОўРЕЦ§ё¶µДИЛКэОЄ![]() Ј¬Фт
Ј¬Фт![]() ЛщУРїЙДЬµДИЎЦµОЄЈє
ЛщУРїЙДЬµДИЎЦµОЄЈє![]()
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]()
![]() µД·ЦІјБРОЄЈє
µД·ЦІјБРОЄЈє
|
|
|
|
|
|
|
|
![]()

 ГыРЈїОМГПµБРґр°ё
ГыРЈїОМГПµБРґр°ёЎѕМвДїЎїК®ИэЅмИ«№ъИЛґу¶юґО»бТйУЪ2019Дк3ФВ5ИХФЪѕ©ХЩїЄ.ОЄБЛБЛЅвДіРЈґуС§Йъ¶ФБЅ»бµД№ШЧўіМ¶ИЈ¬С§РЈГЅМеФЪїЄД»єуµДµЪ¶юМмЈ¬ґУС§ЙъЦРЛж»ъійИЎБЛ180ИЛЈ¬¶ФКЗ·сКХїґ2019ДкБЅ»бїЄД»»бЗйїцЅшРРБЛОКѕнµчІйЈ¬НіјЖКэѕЭµГµЅБРБЄ±нИзПВЈє
КХїґ | Г»КХїґ | єПјЖ | |
ДРЙъ | 40 | ||
Е®Йъ | 30 | 60 | |
єПјЖ |
ЈЁ1Ј©ЗлНкіЙБРБЄ±нЈ»
ЈЁ2Ј©ёщѕЭЙП±нЛµГчЈ¬ДЬ·сУР99%µД°СОХИПОЄёГРЈґуС§ЙъКХїґїЄД»»бУлРФ±рУР№ШЈїЈЁЅб№ыѕ«И·µЅ0.001Ј©
ёЅЈє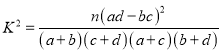 Ј¬ЖдЦР
Ј¬ЖдЦР![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |