Question

直线y=ax+1和双曲线3x²-y²=1相交于A、B两点，问a为何值时，以AB为直径的圆过坐标原点？

Answer 1

解：设A（x₁,y₁）、B（x₂,y₂），因为以AB为直径的圆过坐标原点，

所以OA⊥OB.所以x₁x₂+y₁y₂=0,

即x₁x₂+(ax₁+1)(ax₂+1)=0.

所以（a²+1）x₁x₂+a(x₁+x₂)+1=0.

由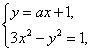得(a²-3)x²+2ax+2=0,

所以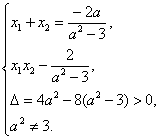

所以a²＜6且a²≠3，（a²+1）·+1=0.

所以a=±1，即当a=±1时，以AB为直径的圆过坐标原点.