题目内容
已知动圆M过定点P(0,m)(m>0),且与定直线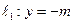 相切,动圆圆心M的轨迹方程为C,直线
相切,动圆圆心M的轨迹方程为C,直线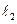 过点P 交曲线C于A、B两点。
过点P 交曲线C于A、B两点。
(1)若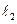 交
交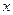 轴于点S,求
轴于点S,求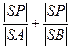 的取值范围;
的取值范围;
(2)若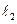 的倾斜角为
的倾斜角为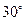 ,在
,在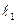 上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.
上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.
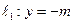 相切,动圆圆心M的轨迹方程为C,直线
相切,动圆圆心M的轨迹方程为C,直线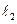 过点P 交曲线C于A、B两点。
过点P 交曲线C于A、B两点。(1)若
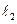 交
交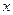 轴于点S,求
轴于点S,求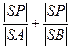 的取值范围;
的取值范围;(2)若
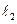 的倾斜角为
的倾斜角为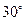 ,在
,在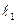 上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.
上是否存在点E使△ABE为正三角形? 若能,求点E的坐标;若不能,说明理由.(1) 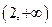 (2)直线l上不存在点E,使得△ABE是正三角形
(2)直线l上不存在点E,使得△ABE是正三角形
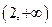 (2)直线l上不存在点E,使得△ABE是正三角形
(2)直线l上不存在点E,使得△ABE是正三角形 (1)依题意,曲线C是以点P为焦点,直线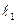 为准线的抛物线,
为准线的抛物线,
所以曲线C的方程为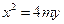 ……(2分)
……(2分)
设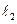 方程为
方程为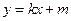 代入
代入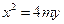 由消去
由消去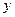 得
得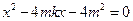
设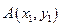 、
、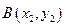 ,则
,则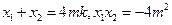 ……(3分)
……(3分)
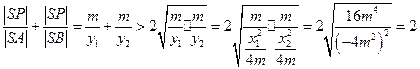
所以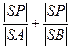 的取值范围是
的取值范围是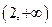 ……(7分)
……(7分)
(2)由(1)知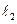 方程为
方程为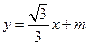 代入
代入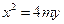 由消去
由消去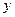 得
得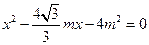
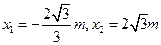 ,
,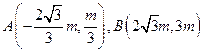 ……(8分)
……(8分)
假设存在点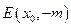 ,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB,……(9分)
,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB,……(9分)
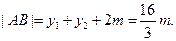 即
即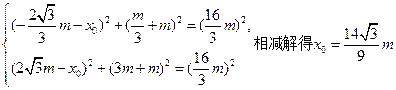 ……(11分)
……(11分)
若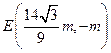 ,则
,则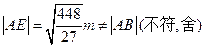
因此,直线l上不存在点E,使得△ABE是正三角形. ……(12分)
解法二:设AB的中点为G,则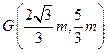 ……(8分)
……(8分)
由 联立
联立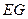 方程
方程
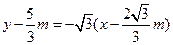 与
与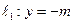 方程求得
方程求得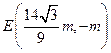 ……(10分)
……(10分)
由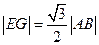 得
得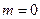 ,矛盾
,矛盾
因此,直线l上不存在点E,使得△ABE是正三角形. ……(12分)
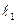 为准线的抛物线,
为准线的抛物线,所以曲线C的方程为
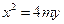 ……(2分)
……(2分)设
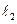 方程为
方程为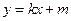 代入
代入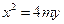 由消去
由消去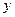 得
得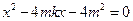
设
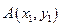 、
、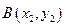 ,则
,则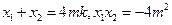 ……(3分)
……(3分)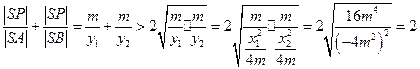
所以
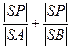 的取值范围是
的取值范围是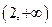 ……(7分)
……(7分)(2)由(1)知
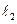 方程为
方程为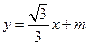 代入
代入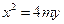 由消去
由消去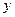 得
得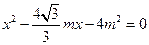
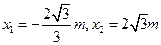 ,
,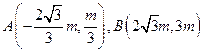 ……(8分)
……(8分)假设存在点
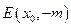 ,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB,……(9分)
,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB,……(9分)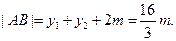 即
即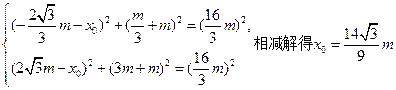 ……(11分)
……(11分)若
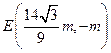 ,则
,则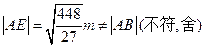
因此,直线l上不存在点E,使得△ABE是正三角形. ……(12分)
解法二:设AB的中点为G,则
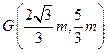 ……(8分)
……(8分)由
 联立
联立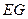 方程
方程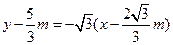 与
与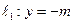 方程求得
方程求得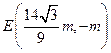 ……(10分)
……(10分)由
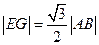 得
得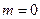 ,矛盾
,矛盾因此,直线l上不存在点E,使得△ABE是正三角形. ……(12分)

练习册系列答案
相关题目
 向圆
向圆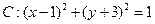 所引的切线方程;
所引的切线方程;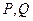 ,求直线
,求直线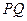 的方程。
的方程。 ,过C点的圆切线与BA的延长线交于E点,证明:
,过C点的圆切线与BA的延长线交于E点,证明:
 的弦AB,使点P为弦AB的中点,则弦AB所在直线方程为 ( )
的弦AB,使点P为弦AB的中点,则弦AB所在直线方程为 ( )




 的圆的方程.
的圆的方程. AC切⊙O于点A,且
AC切⊙O于点A,且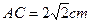 ,过C的割线CMN交
,过C的割线CMN交 .
.
 轴上,且与直线
轴上,且与直线 切于(1,1)点的圆的方程为 。
切于(1,1)点的圆的方程为 。 ,则
,则 的大小为 .
的大小为 .