题目内容
 是函数f(x)=ln(ex+1)+ax为偶函数的
是函数f(x)=ln(ex+1)+ax为偶函数的
- A.充分不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
C
分析:对充分性和必要性分别加以论证:将 代入函数的表达式,不难根据函数奇偶性定义得到函数f(x)为偶函数,从而充分性成立;反之再根据函数为偶函数,用f(x)-f(-x)=0恒成立,采用比较系数法,可得
代入函数的表达式,不难根据函数奇偶性定义得到函数f(x)为偶函数,从而充分性成立;反之再根据函数为偶函数,用f(x)-f(-x)=0恒成立,采用比较系数法,可得 ,说明必要性成立.由此不难选出正确的选项.
,说明必要性成立.由此不难选出正确的选项.
解答:先看充分性
若a=- ,则函数f(x)=ln(ex+1)-
,则函数f(x)=ln(ex+1)- x=ln
x=ln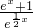 =ln(
=ln(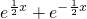 )
)
可得f(-x)=ln(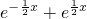 )=f(x),函数是偶函数,充分性成立;
)=f(x),函数是偶函数,充分性成立;
再看必要性
若函数f(x)=ln(ex+1)+ax为偶函数,即
f(-x)=ln(e-x+1)-ax=f(x),
可得ln(ex+1)+ax-(ln(e-x+1)-ax)=0,对任意实数x恒成立
∴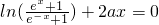 对任意实数x恒成立,
对任意实数x恒成立,
而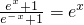 ,上式变成ln(ex)+2ax=(2a+1)x=0对任意实数x恒成立
,上式变成ln(ex)+2ax=(2a+1)x=0对任意实数x恒成立
所以a=- ,可得必要性成立
,可得必要性成立
综上, 是函数f(x)=ln(ex+1)+ax为偶函数的充分必要条件
是函数f(x)=ln(ex+1)+ax为偶函数的充分必要条件
故选C
点评:本题以函数的奇偶性为载体,考查了充分必要条件的判断与证明,属于基础题.在解题过程中将函数进行化简,利用了比较系数的方法求常数a的值,请同学们体会这种常用数学方法.
分析:对充分性和必要性分别加以论证:将
 代入函数的表达式,不难根据函数奇偶性定义得到函数f(x)为偶函数,从而充分性成立;反之再根据函数为偶函数,用f(x)-f(-x)=0恒成立,采用比较系数法,可得
代入函数的表达式,不难根据函数奇偶性定义得到函数f(x)为偶函数,从而充分性成立;反之再根据函数为偶函数,用f(x)-f(-x)=0恒成立,采用比较系数法,可得 ,说明必要性成立.由此不难选出正确的选项.
,说明必要性成立.由此不难选出正确的选项.解答:先看充分性
若a=-
 ,则函数f(x)=ln(ex+1)-
,则函数f(x)=ln(ex+1)- x=ln
x=ln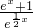 =ln(
=ln(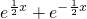 )
)可得f(-x)=ln(
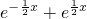 )=f(x),函数是偶函数,充分性成立;
)=f(x),函数是偶函数,充分性成立;再看必要性
若函数f(x)=ln(ex+1)+ax为偶函数,即
f(-x)=ln(e-x+1)-ax=f(x),
可得ln(ex+1)+ax-(ln(e-x+1)-ax)=0,对任意实数x恒成立
∴
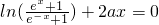 对任意实数x恒成立,
对任意实数x恒成立,而
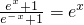 ,上式变成ln(ex)+2ax=(2a+1)x=0对任意实数x恒成立
,上式变成ln(ex)+2ax=(2a+1)x=0对任意实数x恒成立所以a=-
 ,可得必要性成立
,可得必要性成立综上,
 是函数f(x)=ln(ex+1)+ax为偶函数的充分必要条件
是函数f(x)=ln(ex+1)+ax为偶函数的充分必要条件故选C
点评:本题以函数的奇偶性为载体,考查了充分必要条件的判断与证明,属于基础题.在解题过程中将函数进行化简,利用了比较系数的方法求常数a的值,请同学们体会这种常用数学方法.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
规定[x]表示不超过x的最大整数,例如:[3.1]=3,[-2.6]=-3,[-2]=-2;若f′(x)是函数f(x)=ln|x|导函数,设g(x)=f(x)•f′(x),则函数y=[g(x)]+[g(-x)]的值域是( )
| A、{-1,0} | B、{0,1} | C、{0} | D、{偶数} |
设g(x)是函数f(x)=ln(x+1)+2x的导函数,若函数g(x)经过向量
平移后得到函数y=
则向量
=( )( )
| a |
| 1 |
| x |
| a |
| A、(1,2) |
| B、(1,-2) |
| C、(-2,-1) |
| D、(2,1) |