题目内容
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]()
【解析】
试题分析:(1)利用垂径定理得到![]() ,取的中点N,则点M的轨迹是以N为圆心,
,取的中点N,则点M的轨迹是以N为圆心,![]() 为半径的圆
为半径的圆![]() 在圆
在圆![]() 内部的圆弧
内部的圆弧
则点M的轨迹是以N为圆心,![]() 为半径的圆
为半径的圆![]() 在圆
在圆![]() 内部的圆弧.写出圆方程,进一步求得x的取值范围,(2)直线L:y=k(x-4)经过定点R(4,0)过点R作圆
内部的圆弧.写出圆方程,进一步求得x的取值范围,(2)直线L:y=k(x-4)经过定点R(4,0)过点R作圆![]() 的切线,切点为Q,判断切点在圆弧上,又
的切线,切点为Q,判断切点在圆弧上,又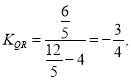
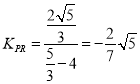 ,所以
,所以![]() .
.
试题解析:(1)取AB的中点M,连接![]() .根据垂径定理有
.根据垂径定理有![]() 即
即![]() .取的中点N
.取的中点N
则点M的轨迹是以N为圆心,![]() 为半径的圆
为半径的圆![]() 在圆
在圆![]() 内部的圆弧.其所在圆的方程为
内部的圆弧.其所在圆的方程为![]() ,联立
,联立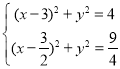 解得
解得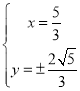 所以C:
所以C:![]()
(2)直线L:y=k(x-4)经过定点R(4,0)过点R作圆![]() 的切线,切点为Q,下面判断切点的横坐标是否在
的切线,切点为Q,下面判断切点的横坐标是否在![]() 内,作出圆
内,作出圆![]() ,C
,C![]() 为的圆心,P为(2)中圆弧上端点,P
为的圆心,P为(2)中圆弧上端点,P![]() 作
作![]() ,则由相似三角形得,
,则由相似三角形得,![]()
![]() 而
而![]() 所以切点Q在(2)求得的圆弧上,又
所以切点Q在(2)求得的圆弧上,又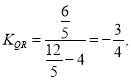
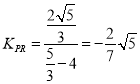 ,所以
,所以![]() .
.

练习册系列答案
相关题目