题目内容
【题目】函数 ![]() 的部分图象如图所示,求:
的部分图象如图所示,求: 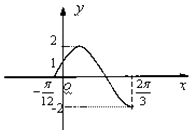
(1)f(x)的表达式.
(2)f(x)的单调增区间.
(3)f(x)的最小值以及取得最小值时的x集合.
【答案】
(1)解:根据函数 ![]() 的部分图象,
的部分图象,
可得A=2, ![]() =
= ![]() +
+ ![]() ,求得ω=2,∴f(x)=2sin(2x+φ).
,求得ω=2,∴f(x)=2sin(2x+φ).
再根据五点法作图可得2 ![]() +φ=
+φ= ![]() ,∴φ=
,∴φ= ![]() ,∴f(x)=2sin(2x+
,∴f(x)=2sin(2x+ ![]() )
)
(2)解:令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(3)解:令2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() ,求得x=kπ+﹣
,求得x=kπ+﹣ ![]() ,可得当x=kπ+﹣
,可得当x=kπ+﹣ ![]() ,k∈Z 时,函数取得最小值为﹣2.
,k∈Z 时,函数取得最小值为﹣2.
即f(x)的最小值为﹣2,取得最小值时的x集合为{x|x=kπ+﹣ ![]() ,k∈Z }
,k∈Z }
【解析】(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)利用正弦函数的单调性,求得函数的增区间.(3)利用正弦函数的最值,求得f(x)的最小值以及取得最小值时的x集合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

