题目内容
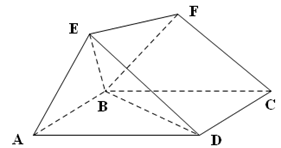
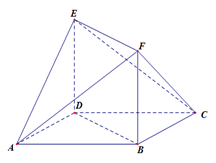
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且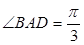 ,以
,以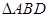 与
与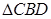 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥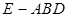 与
与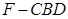 ,且
,且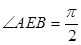 .
.
(1)求证: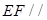 平面
平面 ;
;
(2)求平面 与平面
与平面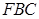 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
(1)证明过程见解析;(2)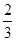 .
.
解析试题分析:(1)作 面
面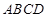 于
于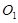 ,作
,作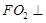 面
面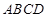 于
于 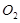 ,易得四边形
,易得四边形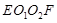 是平行四边形,所以
是平行四边形,所以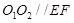 .又
.又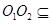 面
面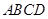 ,
,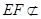 面
面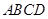 ,所以
,所以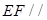 平面
平面 ;
;
(2)以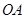 为
为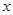 轴的正方向,以
轴的正方向,以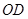 为
为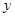 轴的正方向,在平面
轴的正方向,在平面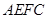 中过
中过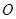 点作面
点作面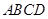 的垂线为
的垂线为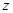 轴,建立空间直角坐标系求题,利用向量,求出平面
轴,建立空间直角坐标系求题,利用向量,求出平面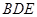 和平面
和平面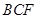 的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
的法向量,则两平面的法向量的夹角即为所求角或为所求角的补角.
(1)作 面
面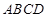 于
于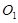 ,作
,作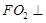 面
面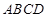 于
于 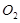 ,因
,因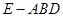 与
与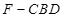 都是正三棱锥, 且
都是正三棱锥, 且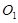 、
、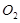 分别为
分别为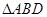 与
与 的中心,
的中心,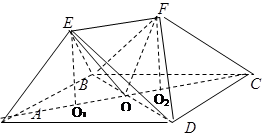
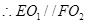 且
且 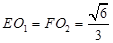 .
.
所以四边形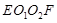 是平行四边形,所以
是平行四边形,所以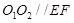 .
.
又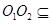 面
面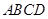 ,
,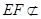 面
面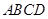 ,所以
,所以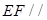 平面
平面
(2)如图,建立空间直角坐标系,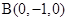 、
、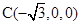 、
、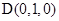 、
、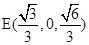 、
、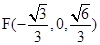 .
. 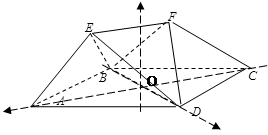
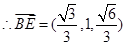 、
、 、
、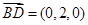 、
、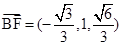 .…7分
.…7分
设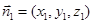 为平面
为平面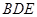 的法向量,
的法向量,
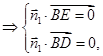
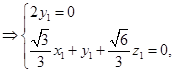

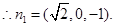
设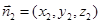 为平面
为平面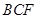 的法向量,
的法向量,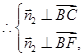
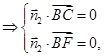

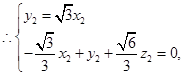
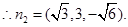 &nbs
&nbs

练习册系列答案
相关题目
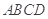 是正方形,
是正方形,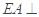 平面
平面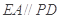 ,
,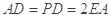 ,
,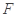 ,
,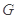 ,
, 分别为
分别为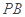 ,
,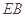 ,
,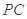 的中点.
的中点.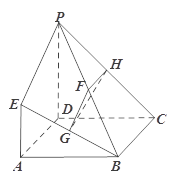
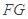
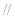 平面
平面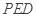 ;
;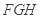 与平面
与平面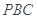 所成锐二面角的大小.
所成锐二面角的大小.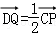 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.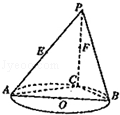
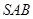 所在平面与直角梯形
所在平面与直角梯形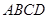 所在平面垂直,且
所在平面垂直,且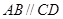 ,
,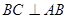 ,
,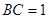 ,
,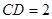 ,
,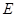 、
、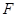 分别是线段
分别是线段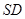 、
、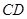 的中点.
的中点.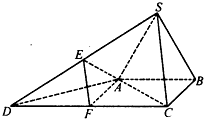
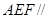 平面
平面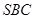 ;
;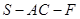 的余弦值.
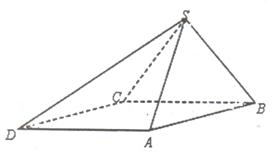
的余弦值. 底面ABCD.已知
底面ABCD.已知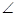 ABC=45o,AB=2,BC=2
ABC=45o,AB=2,BC=2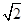 ,SA=SB=
,SA=SB=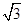 .
.
 ,
,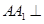 平面
平面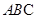 ,
,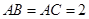 ,
,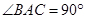 ,四边形
,四边形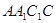 为正方形,
为正方形,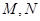 分别为
分别为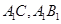 中点.
中点.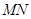 ∥面
∥面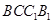 ;
; —
—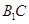 —
—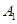 的余弦值.
的余弦值.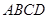 是菱形,
是菱形,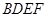 是矩形,
是矩形,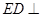 平面
平面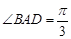 ,
,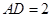 .
.
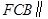 平面
平面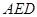 ;
;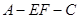 为直二面角,求直线
为直二面角,求直线 与平面
与平面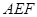 所成的角
所成的角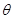 的正弦值.
的正弦值.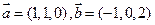 ,若向量
,若向量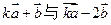 互相垂直,则
互相垂直,则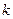 的值为 。
的值为 。