题目内容
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC 底面ABCD.已知
底面ABCD.已知 ABC=45o,AB=2,BC=2
ABC=45o,AB=2,BC=2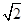 ,SA=SB=
,SA=SB=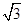 .
.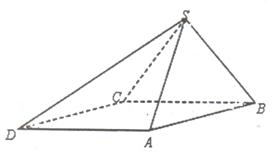
(1)证明:SA BC;
BC;
(2)求直线SD与平面SAB所成角的正弦值.
(1)详见解析,(2)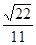 .
.
解析试题分析:(1)已知条件为面面垂直,因此由面面垂直性质定理转化为线面垂直. 作 ,由侧面
,由侧面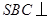 底面
底面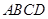 ,得
,得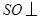 平面
平面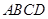 .证明线线垂直,有两个思路,一是通过线面垂直转化,二是利用空间向量计算.本题考虑到第二小题,采取空间向量方法. 利用空间向量以算代证,关键正确表示各点及对应向量的坐标,利用空间向量数量积进行论证.(2)利用空间向量求线面角,关键正确求出平面的一个法向量,利用两向量夹角的余弦值的绝对值等于线面角的正弦值的等量关系进行求解.
.证明线线垂直,有两个思路,一是通过线面垂直转化,二是利用空间向量计算.本题考虑到第二小题,采取空间向量方法. 利用空间向量以算代证,关键正确表示各点及对应向量的坐标,利用空间向量数量积进行论证.(2)利用空间向量求线面角,关键正确求出平面的一个法向量,利用两向量夹角的余弦值的绝对值等于线面角的正弦值的等量关系进行求解.
试题解析:(1)作 ,垂足为
,垂足为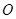 ,连结
,连结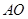 ,
,
由侧面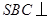 底面
底面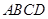 ,
,
得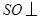 平面
平面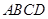 ..2
..2
因为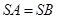 ,所以
,所以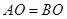 3
3
又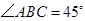 ,
,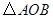 为等腰直角三角形,
为等腰直角三角形,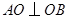 4
4
如图,以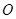 为坐标原点,
为坐标原点,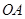 为
为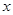 轴正向,建立直角坐标系
轴正向,建立直角坐标系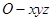 .
.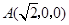 ,
,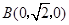 ,
,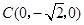 ,
,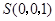 ,
, 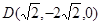 6
6 ,
,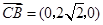 ,
,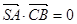 ,所以
,所以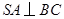 8
8
(2)设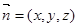 为平面SAB的法向量
为平面SAB的法向量
则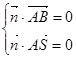 得
得 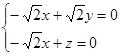 所以
所以 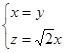
令x=1 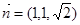 10
10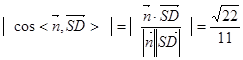 12
12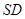 与平面
与平面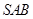 所成的角与
所成的角与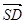 与
与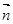 所成的角互余.
所成的角互余.
所以,直线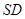 与平面
与平面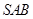 所成的角正弦值为
所成的角正弦值为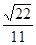 13
13
考点:面面垂直性质定理,空间向量求证线线垂直,空间向量求线面角

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 分别是正三棱柱
分别是正三棱柱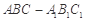 的棱
的棱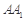 、
、 的中点,且棱
的中点,且棱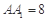 ,
,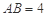 .
.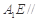 平面
平面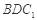 ;
;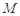 ,使二面角
,使二面角 的大小为
的大小为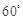 ,若存在,求
,若存在,求 的长,若不存在,说明理由。
的长,若不存在,说明理由。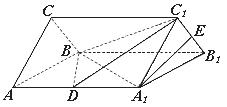
 平面
平面 ,
,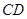 ∥
∥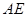 ,
,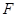 是
是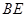 的中点,
的中点,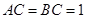 ,
,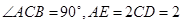 .
.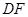 ∥平面
∥平面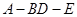 的大小的余弦值.
的大小的余弦值.
 是边长为2的菱形,且
是边长为2的菱形,且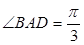 ,以
,以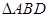 与
与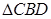 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥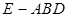 与
与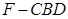 ,且
,且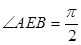 .
.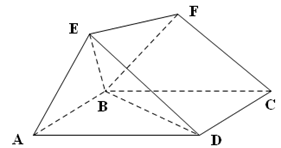
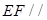 平面
平面 与平面
与平面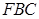 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.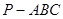 中,直线
中,直线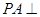 平面
平面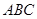 ,且
,且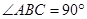 ,又点
,又点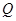 ,
,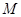 ,
,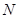 分别是线段
分别是线段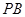 ,
,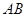 ,
,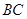 的中点,且点
的中点,且点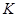 是线段
是线段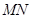 上的动点.
上的动点.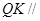 平面
平面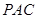 ;
;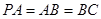 ,求二面角
,求二面角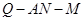 的平面角的余弦值.
的平面角的余弦值.
 ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN= BD.
BD. ,求线段MN的长度.
,求线段MN的长度.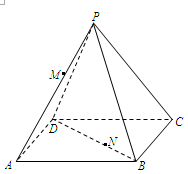
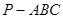 中,直线
中,直线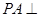 平面
平面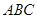 ,且
,且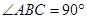 ,又点
,又点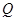 ,
, ,
,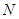 分别是线段
分别是线段 ,
,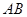 ,
,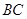 的中点,且点
的中点,且点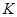 是线段
是线段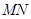 上的动点.
上的动点.
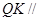 平面
平面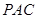 ;
;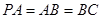 ,求二面角
,求二面角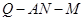 的平面角的余弦值.
的平面角的余弦值. 沿AF折起,得到如图所示的三棱锥
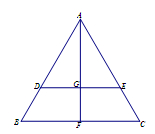
沿AF折起,得到如图所示的三棱锥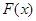 ,其中
,其中 .
.
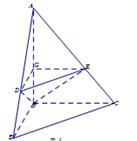
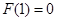 //平面
//平面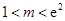 ;
;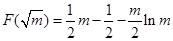 ;
;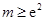 时,求三棱锥
时,求三棱锥